
Cách sửa lỗi iPhone bị loạn cảm ứng hiệu quả sau 5 phút
Các cách khắc phục lỗi loạn cảm ứng trên iPhone mà bạn không nên bỏ qua!
Người dùng iPhone thường gặp một tình trạng chung đó là loạn cảm ứng, điều này ảnh hưởng rất nhiều đến trải nghiệm. Vậy nguyên nhân của loạn cảm ứng trên điện thoại nhà Apple là do đâu? Cách khắc phục như thế nào? Tất cả sẽ có trong bài biết bên dưới, tham khảo ngay nhé!
Nguyên nhân iPhone bị loạn cảm ứng
Ghost Touch là tên gọi khác của tình trạng loạn cảm ứng trên iPhone. Đâu là hiện tượng mà người dùng không thể điều khiển các tính năng trên màn hình điện thoại theo ý mình. Mặc dù không thực hiện thao tác hay nhấn vào màn hình cảm ứng nhưng nó vẫn nhảy loạn xạ. Ngay lúc này những ứng dụng trên điện thoại sẽ tự động tắt/ bật liên tục, đồng thời phiền phức cho người sử dụng. Được biết, có khá nhiều nguyên nhân dẫn đến tình Ghost Touch, tương ứng với một cách khắc phục khác nhau.

Dưới đây là một số nguyên nhân:
- Cùng một lúc người dùng mở nhiều ứng dungj làm cho iPhone không xử lý kịp, khi đó máy sẽ nóng nhanh và xuất hiện tình trạng lỗi cảm ứng.
- Người dùng là rơi, vỡ, va đập mạnh iPhone nên gây ra hiện tượng Ghost Touch
- Các dây sạc, củ sạc không phải chính hãng, hàng chất lượng kém cũng dẫn đến lỗi iPhone bị loạn cảm ứng lúc sạc.
- Sử dụng miếng dán cường lực có chất lượng không tốt cũng dễ dẫn đến tình trạng điện thoại Apple gặp lỗi Ghost Touch.
- Một vài xung đột của các phần mềm bên trong cũng làm cho iPhone loạn cảm ứng.
- Điện thoại Apple đặt tại nơi ẩm thấp, ít thông thoáng hoặc bị dính nước cũng ảnh hưởng đến chức năng cảm ứng.
- iPhone bị lỗi hệ điều hành iOS cũng làm cho màn hình đơ hoặc loạn cảm ứng.
Cách sửa lỗi iPhone bị loạn cảm ứng
Như đã thấy, có khá nhiều nguyên nhân dẫn đến tình trạng loạn cảm ứng trên iPhone. Khi xác định được chính xác lý do, người dùng sẽ có cách xử lý tương ứng, cụ thể như sau:
Vệ sinh màn hình cảm ứng
Khi gặp lỗi Ghost Touch, việc đầu tiên chúng ta cần làm là vệ sinh sạch màn hình, điều này làm loại bỏ những bụi bẩn hay vật thể lạ bám trên bà mặt. Để thực hiện, trước tiên nên tháo tất cả dây cáp kết nối với iPhone và tắt máy, sau đó làm ẩm miếng vải mền và làm sạch, cuối cùng là lau khô để loại bỏ tất cả bụi bẩn.

Lưu ý:
- Không dùng khăn quá ướt để lau, điều này làm nước chảy vào các khe hở trên iPhone.
- Không sử dùng chất tẩy rửa hoặc dung dịch có tính mài mòn để vệ sinh màn hình iPhone, vì nó làm bay đi lớp chống dầu phủ trên màn hình.
Kiểm tra pin
Khi pin yếu hoặc cạn kiệt cũng là nguyên nhân khiến iPhone bị lỗi cảm ứng. Vì vậy hãy sạc đầy pin và kiểm tra xem sự cố cảm biến đã được giải quyết chưa.
Lưu ý: Để kéo dài tuổi thọ cho pin iPhone, bạn cần hạn chế tình trạng hao mòn pin. Bạn nên sạc điện thoại ngay khi pin sắp tụt xuống dưới 20%. Sạc pin khi hết dung lượng và tắt nguồn có thể ảnh hưởng xấu đến tuổi thọ của pin.
Tháo ốp lưng
Khi sử dụng điện thoại, nhiều người thích dùng ốp lưng dẻo và liên tục tháo ra lắp lại. Điều này vô tình khiến màn hình cảm ứng bị biến dạng và gây ra lỗi cảm ứng. Nếu bạn có thói quen này và iPhone của bạn gần đây gặp lỗi Ghost Touch thì bạn nên tháo ốp lưng ra ngay.

Tháo cường lực
Kính cường lực iPhone là một lớp kính bảo vệ mỏng được phủ lên màn hình cảm ứng nguyên bản. Nó giúp ngăn chặn màn hình gốc bị nứt, vỡ và trầy xước màn hình. Nhưng đôi khi lực tác động khiến iPhone Ghost Touch. Nếu bạn gặp lỗi loạn cảm ứng trên iPhone, hãy thử tháo cường lực.
Cách dễ nhất để thực hiện việc này là bóc kính cường lực ra khỏi bất kỳ góc nào của màn hình. Tiếp theo, bạn tháo toàn bộ kính khỏi màn hình iPhone. Nếu không làm được hoặc tình trạng kính cường lực bị vỡ quá nghiêm trọng hãy mang đến cửa hàng sửa chữa điện thoại uy tín. Họ sẽ giúp bạn bóc kính cường lực một cách an toàn.
Cập nhật phần mềm
Sử dụng phiên bản iOS quá cũ có thể gây ra sự cố cảm ứng trên iPhone. Để thực hiện cập nhật phần mềm trên iPhone, hãy làm theo các bước sau:
- Bước 1: Vào Cài đặt trên iPhone. Sau đó bấm vào Cài đặt chung.
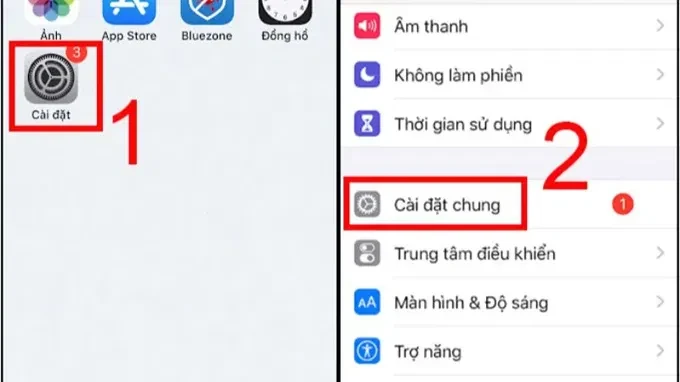
- Bước 2: Tiếp tục nhấn Install Software. Sau đó bạn chọn Cập nhật tự động hoặc Tải xuống.
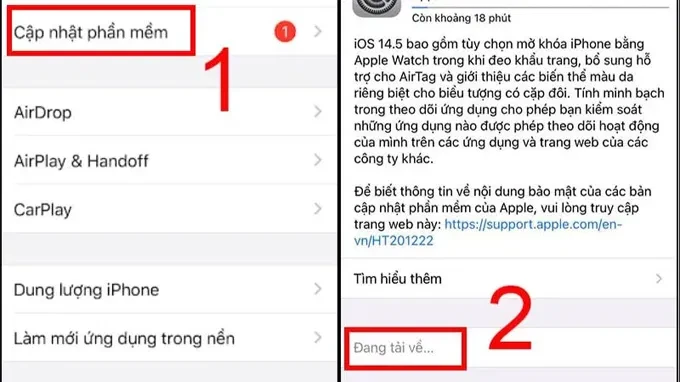
Khởi động iPhone
Đây là giải pháp được nhiều người thực hiện ngay khi gặp lỗi Ghost Touch trên iPhone. Để nhanh chóng khởi động lại thiết bị, bạn có thể sử dụng các phím cứng trên điện thoại. Cụ thể:
- Với iPhone 6s hoặc 6s Plus trở về trước, bạn chỉ cần nhấn và giữ phím nguồn và phím home cho đến khi xuất hiện quả táo trên màn hình.
- Với iPhone 7 hoặc 7 plus, bạn chỉ cần nhấn giữ đồng thời phím nguồn và phím giảm âm lượng cho đến khi hiện quả táo.
- Từ iPhone 8 trở lên, bạn chỉ cần nhấn và thả nhanh nút tăng giảm âm lượng, sau đó giữ nút nguồn cho đến khi xuất hiện quả táo trên màn hình.
- Từ iPhone X trở về sau, bạn phải làm là kéo biểu tượng tắt nguồn sang phải để tắt nguồn.
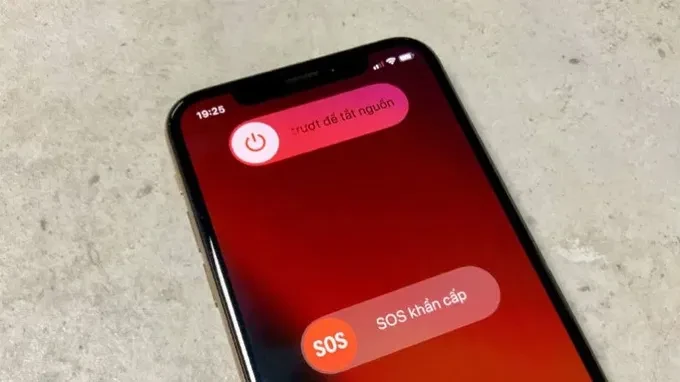
Sau khi tắt iPhone bằng các cách trên, bạn chỉ cần giữ nút nguồn để khởi động lại iPhone. Khi đó bạn có thể xem lỗi cảm ứng iPhone đã được khắc phục chưa.
Reset iPhone
Nếu người dùng đã áp dụng các cách trên mà vẫn không khắc phục được lỗi cảm ứng thì bạn cần reset iPhone, cụ thể như sau:
- Bước 1: Vào “Cài đặt” và chọn “Cài đặt chung”.
- Bước 2: Kéo xuống dưới và chọn “Chuyển hoặc đặt lại iPhone”.
- Bước 3: Chọn “Đặt lại và chọn Đặt lại tất cả cài đặt”.
Hong khô iPhone
Dưới đây là cách khắc phục lỗi Ghost Touch trên iPhone nếu bạn cho rằng nguyên nhân là do điện thoại tiếp xúc với nước. Trước tiên, hãy lau bên ngoài iPhone của bạn bằng vải mềm. Tiếp theo, sử dụng máy sấy để làm khô iPhone của bạn. Sau đó tháo các phụ kiện như nắp lưng, thẻ SIM, nắp cổng điện thoại để máy thoát nước. Cuối cùng, hãy đặt iPhone của bạn lên một chiếc khăn mềm và để ở nơi khô ráo để khô tự nhiên trong 48 giờ.

Kiểm tra cáp sạc
Khi bạn sử dụng cáp sạc một thời gian và nhận thấy pin iPhone của mình sạc chậm hoặc sạc yếu, lag khi cắm vào thì rất có thể bộ sạc của bạn đã bị lỗi chất lượng. Vì vậy mọi người nên chuyển sang cáp sạc khác để sạc đầy pin nhé. Sau đó bạn rút sạc ra để sử dụng xem lỗi cảm ứng còn tồn tại hay không.
Kiểm tra nguồn điện
Khi bạn sử dụng sạc dự phòng không đảm bảo chất lượng hoặc sạc không chính hãng. Đây cũng chính là nguyên nhân khiến cảm ứng của iPhone bị loạn cảm ứng. Lúc này bạn cần mua pin thay thế hoặc sạc dự phòng chính hãng tương ứng với từng phiên bản.

Đem iPhone tới trung tâm bảo hành hoặc cửa hàng ủy quyền
Nếu đã thử tất cả các cách khắc phục trên mà tình trạng Ghost Touch trên iPhone vẫn tồn tại, bạn có thể mang iPhone đến trung tâm bảo hành hoặc cửa hàng ủy quyền của Apple. Họ sẽ tư vấn cho bạn và sửa lỗi nhanh chóng. Ngoài ra, bạn sẽ nhận được sự tư vấn tận tình về tình trạng iPhone của mình và được hưởng những chính sách bảo hành tốt nhất cho sản phẩm khi đến các trung tâm hoặc cửa hàng Apple. Để tiết kiệm chi phí sửa iPhone bị lỗi loạn cảm ứng, bạn có thể kiểm tra xem điện thoại của mình còn bảo hành hay không để sửa chữa nhanh chóng.
Bài viết trên đã đưa ra 8 cách khắc phục lỗi cảm ứng iPhone mà bất cứ ai cũng có thể học hỏi. Việc có một chiếc iPhone bị lỗi cảm ứng sẽ gây ra rất nhiều khó khăn cho công việc của bạn. Do đó, những biện pháp trên có thể giúp mọi người sử dụng iPhone mượt mà hơn.
Xem thêm:
- iPhone 17 có thể sẽ được Apple trang bị màn hình hiện đại hơn
- Apple đang phát triển chip 5G cho iPhone 17 Slim và iPhone SE 4
- iPhone 17 Plus sẽ bị huỷ bỏ, model nào sẽ thay thế?
XTmobile.vn
Link nội dung: https://galileo.edu.vn/cach-sua-loi-iphone-bi-loan-cam-ung-hieu-qua-sau-5-phut-a13675.html