Tam giác vuông là một phần quan trọng trong hình học, không chỉ vì tính chất đặc biệt của nó mà còn vì những ứng dụng rộng rãi trong đời sống và toán học. Trong bài viết này, chúng ta sẽ cùng nhau khám phá các cách chứng minh tam giác vuông, từ khái niệm cơ bản cho đến các trường hợp bằng nhau của tam giác vuông.
1. Khái Niệm Về Tam Giác Vuông
Tam giác vuông là một tam giác có một góc bằng 90 độ. Các cạnh bên, trong đó một cạnh tạo thành góc vuông gọi là
cạnh góc vuông, còn cạnh đối diện với góc vuông gọi là
cạnh huyền. Tam giác vuông rất đặc biệt vì nó có nhiều tính chất có thể được ứng dụng trong việc chứng minh hình học.
1.1 Đặc Điểm Của Tam Giác Vuông
- Góc Vuông: Có một góc bằng 90 độ.
- Định lý Pythagore: Tổng bình phương của hai cạnh góc vuông bằng bình phương của cạnh huyền.
- Tính chất đồng dạng: Hai tam giác vuông có thể đồng dạng nếu có các cạnh và góc tương ứng bằng nhau.
2. Các Trường Hợp Bằng Nhau Của Tam Giác Vuông
Khi đề cập đến hai tam giác vuông, có nhiều trường hợp mà chúng có thể được coi là bằng nhau. Dưới đây là các trường hợp chính.
2.1 Bằng Nhau Theo Cạnh - Góc - Cạnh (C.G.C)
Hai tam giác vuông được coi là bằng nhau nếu có một cạnh góc vuông và một góc kề với cạnh đó lần lượt bằng một cạnh góc vuông và một góc kề với cạnh đó của tam giác kia.
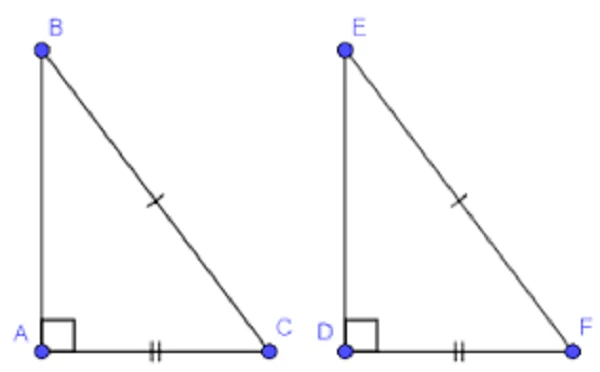
2.2 Bằng Nhau Theo Cạnh Huyền - Cạnh Góc Vuông (H.C)
Tam giác vuông được coi là bằng nhau nếu một cạnh huyền của tam giác này bằng một cạnh huyền của tam giác kia và có một trong hai cạnh góc vuông tương ứng cũng bằng nhau.
2.3 Bằng Nhau Theo Hai Cạnh Góc Vuông (C.G)
Nếu hai cạnh góc vuông của tam giác này lần lượt bằng hai cạnh góc vuông của tam giác còn lại, chúng ta có thể chứng minh rằng hai tam giác đó bằng nhau.
2.4 Bằng Nhau Theo Cạnh Huyền Và Góc Nhọn (H.G)
Hai tam giác vuông được gọi là bằng nhau nếu cạnh huyền và một góc nhọn của tam giác này bằng cạnh huyền và một góc nhọn của tam giác kia.
3. Cách Chứng Minh Hai Tam Giác Vuông Bằng Nhau
Để chứng minh hai tam giác vuông bằng nhau, người học cần phân tích và kiểm tra các điều kiện cùng một lúc. Dưới đây là các bước chi tiết.
3.1 Xác Định Các Điều Kiện Cần Thiết
- Kiểm tra các cạnh: Xem xét xem liệu các cạnh góc vuông và cạnh huyền của cả hai tam giác có cùng độ dài hay không.
- Xác định các góc: Kiểm tra xem các góc tương ứng có bằng nhau không, đặc biệt là góc vuông.
3.2 Sử Dụng Định Lý Pythagore
Nếu cần, sử dụng định lý Pythagore để chứng minh rằng hai tam giác có cùng độ dài cạnh huyền. Công thức Pythagore thể hiện rõ mối quan hệ giữa ba cạnh của tam giác vuông.
3.3 Áp Dụng Tính Chất Đồng Dạng
Nếu xác định được hai tam giác có cùng một số cạnh và góc bằng nhau, có thể sử dụng tính chất đồng dạng để rút ra kết luận.
4. Ví Dụ Minh Họa Cách Chứng Minh Tam Giác Vuông
Dưới đây là một số ví dụ cụ thể giúp bạn hiểu rõ hơn về cách chứng minh các tam giác vuông bằng nhau.
4.1 Ví Dụ 1: Chứng Minh Cạnh Vuông Bằng Nhau
Cho tam giác vuông ABC và DEF, biết rằng:
- Góc A = góc D = 90 độ
- AC = DF
Nếu cho AB = DE thì chúng ta có thể chứng minh rằng ΔABC = ΔDEF bằng cách áp dụng trường hợp C.G.C.
4.2 Ví Dụ 2: Chứng Minh Góc Và Đoạn Thẳng Bằng Nhau
Xét hai tam giác vuông GHI và JKL, với:
- GH = JK
- IG = JL
- Góc H = góc K
Chúng ta có thể xác định rằng ΔGHI = ΔJKL chứng minh qua các điều kiện góc-góc-cạnh.
5. Bài Tập Thực Hành
Để củng cố kiến thức, người học có thể thử sức với một số bài tập sau:
5.1 Bài Tập Lý Thuyết
- Liệt kê các trường hợp bằng nhau của tam giác vuông.
- Trình bày và minh họa định lý Pythagore.
- Đưa ra khái niệm tam giác vuông và nêu rõ các đặc điểm của nó.
5.2 Bài Tập Thực Hành
- Chứng minh rằng hai tam giác vuông giống nhau dựa vào các thông tin cho trước.
- Tìm các điều kiện cần thiết để hai tam giác vuông bằng nhau theo từng trường hợp.
6. Kết Luận
Chứng minh tam giác vuông không hề khó nếu bạn nắm vững các khái niệm và trường hợp bằng nhau của chúng. Bằng việc áp dụng các phương pháp một cách linh hoạt, bạn có thể giải quyết được nhiều bài toán hình học liên quan đến tam giác vuông.
Hy vọng rằng bài viết này sẽ giúp bạn có thêm kiến thức và tự tin hơn trong việc làm các bài tập hình học về tam giác vuông. Hãy luyện tập đều đặn để cải thiện khả năng suy luận và logic của mình nhé!













