Khám Phá Vấn Đề Tài Chính Qua Các Tính Toán Thực Tiễn
Trong lĩnh vực tài chính cá nhân và doanh nghiệp, có một khía cạnh không thể thiếu đó chính là việc tính toán các khoản tiền lãi. Những con số này không chỉ đơn thuần là một phần của các giao dịch ngân hàng mà còn là dấu hiệu cho sự phát triển của mọi kế hoạch đầu tư. Để hiểu rõ hơn về vấn đề này, chúng ta sẽ cùng nhau khám phá các dạng bài toán phổ biến, từ đó rút ra các công thức hữu ích để áp dụng vào thực tế.

H2: Các Dạng Bài Toán Cơ Bản
Bắt đầu từ những bài toán cơ bản, một trong những loại bài toán phổ biến nhất là bài toán liên quan đến lãi suất đơn. Đây là loại bài toán rất thường xuất hiện trong các bài kiểm tra, đặc biệt là trong kỳ thi trung học phổ thông.
Bài Toán Lãi Suất Đơn
Công thức tính lãi suất đơn là:
\[ L = P \times r \times t \]
Trong đó:
- \( L \) là số tiền lãi.
- \( P \) là số tiền gốc (số tiền ban đầu).
- \( r \) là lãi suất (theo dạng thập phân).
- \( t \) là thời gian (tính bằng năm).
Ví dụ minh họa
Giả sử bạn gửi vào ngân hàng 100 triệu đồng với lãi suất 5% trong 2 năm. Số tiền lãi bạn nhận được sẽ là:
\[ L = 100,000,000 \times 0.05 \times 2 = 10,000,000 \, (đồng) \]
Bài Toán Lãi Suất Kép
Tiếp đến là lãi suất kép, một khái niệm rất quan trọng trong tài chính. Công thức tính lãi suất kép như sau:
\[ A = P \times (1 + r)^n \]
Trong đó:
- \( A \) là số tiền cuối cùng (sau khi tính cả vốn lẫn lãi).
- \( P \) là số tiền gốc.
- \( r \) là lãi suất (theo dạng thập phân).
- \( n \) là số kỳ hạn (năm).
Ví dụ minh họa
Nếu bạn gửi 100 triệu đồng vào ngân hàng với lãi suất 5% trong 3 năm, số tiền cuối cùng bạn sẽ có là:
\[ A = 100,000,000 \times (1 + 0.05)^3 \]
\[ A = 100,000,000 \times 1.157625 = 115,762,500 \, (đồng) \]

H2: Phân Tích Chi Tiết Từng Dạng Bài Toán
Dạng Bài Toán Về Tiền Gửi
Một dạng bài toán rất phổ biến là bài toán về tiền gửi ngân hàng. Trong đó, mỗi tháng bạn gửi vào ngân hàng một số tiền cố định, và lãi suất cũng được tính theo tháng.
Công thức tính
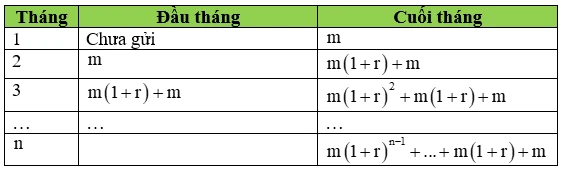
Nếu bạn gửi \( m \) triệu đồng mỗi tháng với lãi suất \( r\% \) mỗi tháng trong \( n \) tháng, số tiền thu được sẽ là:
\[ A = m \times \frac{(1 + r)^n - 1}{r} \]
Ví dụ minh họa
Giả sử bạn gửi 5 triệu đồng mỗi tháng vào ngân hàng với lãi suất 1% mỗi tháng trong 12 tháng. Số tiền cuối cùng bạn nhận được sẽ là:
\[ A = 5 \times \frac{(1 + 0.01)^{12} - 1}{0.01} \]
\[ A = 5 \times \frac{1.126825 - 1}{0.01} = 5 \times 12.6825 \approx 63.4125 \, (triệu đồng) \]
Dạng Bài Toán Về Vay Ngân Hàng
Ngoài tiền gửi, bài toán về vay ngân hàng cũng rất phổ biến. Khi đi vay, bạn sẽ phải trả lãi hàng tháng hoặc hàng năm, và đôi khi còn cả vốn.
Công thức tính
Nếu bạn vay \( P \) triệu đồng với lãi suất \( r\% \) mỗi tháng và kỳ hạn vay là \( n \) tháng, số tiền lãi bạn phải trả hàng tháng sẽ là:
\[ L = \frac{P \times r}{100} \]
Ví dụ minh họa
Giả sử bạn vay 200 triệu đồng với lãi suất 6% mỗi năm và kỳ hạn vay là 2 năm. Mỗi tháng, bạn sẽ phải trả:
\[ L = \frac{200 \times 6 / 12}{100} = 1 triệu đồng \]
H2: Lời Khuyên Khi Thực Hiện Các Tính Toán Tài Chính
Lập Kế Hoạch Tài Chính
Trước khi thực hiện bất kỳ loại giao dịch tài chính nào, hãy lập một kế hoạch rõ ràng về cách bạn sẽ sử dụng số tiền và cách bạn sẽ trả nợ nếu có.
Đọc Kỹ Điều Khoản Hợp Đồng
Khi vay hay gửi tiền, hãy đọc kỹ điều khoản hợp đồng, đặc biệt là các thông tin liên quan đến lãi suất, các khoản phí và điều kiện thanh toán.
Tìm Hiểu Thêm Về Các Công Cụ Tài Chính
Đừng ngần ngại tìm hiểu thêm về các sản phẩm tài chính khác nhau, từ chứng khoán đến bất động sản, để có cái nhìn toàn diện hơn về tài chính cá nhân.
Kết Luận
Bài toán về lãi suất không chỉ là một phần của toán học mà còn là một phần quan trọng trong cuộc sống hàng ngày. Việc hiểu rõ và áp dụng đúng các công thức sẽ giúp bạn quản lý tài chính cá nhân hiệu quả hơn. Hy vọng rằng với những thông tin và ví dụ thực tiễn ở trên, bạn đã có thêm kiến thức bổ ích để áp dụng vào các tình huống tài chính trong tương lai. Hãy luôn nhớ rằng, việc lên kế hoạch và tính toán chính xác sẽ mang lại thành công trong mọi giao dịch tài chính của bạn.

















