Tứ diện không chỉ là một khái niệm hình học cơ bản trong chương trình học, mà còn là một chủ đề thú vị trong toán học không gian. Bài viết dưới đây sẽ giúp bạn hiểu rõ hơn về tứ diện, bao gồm tứ diện đều, các tính chất, công thức tính toán và nhiều bài tập ứng dụng để minh họa cho những kiến thức lý thuyết.
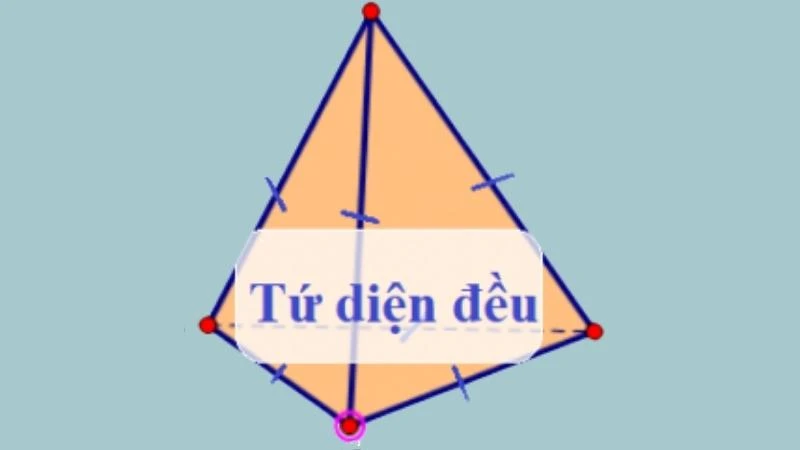
Tứ Diện Là Gì?
Tứ diện là một dạng khối đa diện trong không gian, có bốn đỉnh và được hình thành từ bốn điểm không nằm trên cùng một mặt phẳng. Bốn đỉnh này thường được ký hiệu là A, B, C, D, và mỗi đỉnh có thể được xem như là đỉnh của khối hình.
Cách hiểu về tứ diện:
- Nếu bạn coi A là đỉnh, thì mặt tam giác đối diện với A (BCD) được gọi là đáy của tứ diện.
- Nguyên lý là, trong không gian, nếu bạn có bốn điểm A, B, C, D không đồng phẳng với nhau, thì tứ diện ABCD sẽ được tạo thành.
Hình ảnh bên dưới sẽ minh họa rõ hơn về cấu trúc của tứ diện.
Tứ Diện Đều Là Gì?
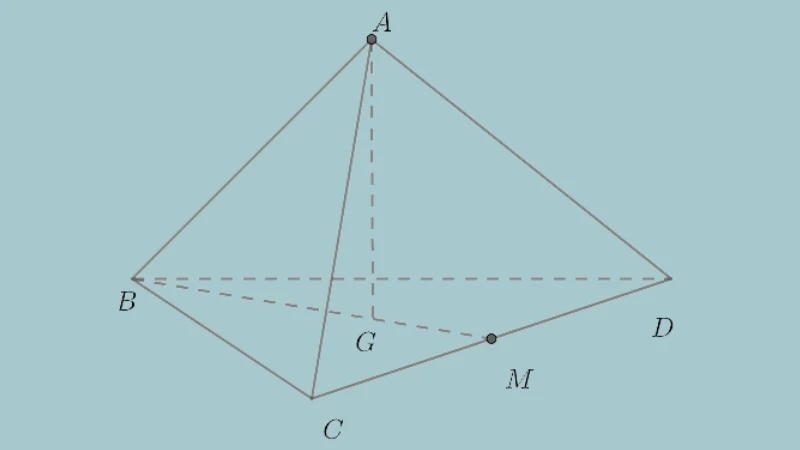
Định Nghĩa
Tứ diện đều là một hình chóp tam giác, trong đó tất cả các mặt xung quanh đều là các tam giác đều. Đặc điểm chính của tứ diện đều là tất cả các cạnh đều có độ dài bằng nhau.
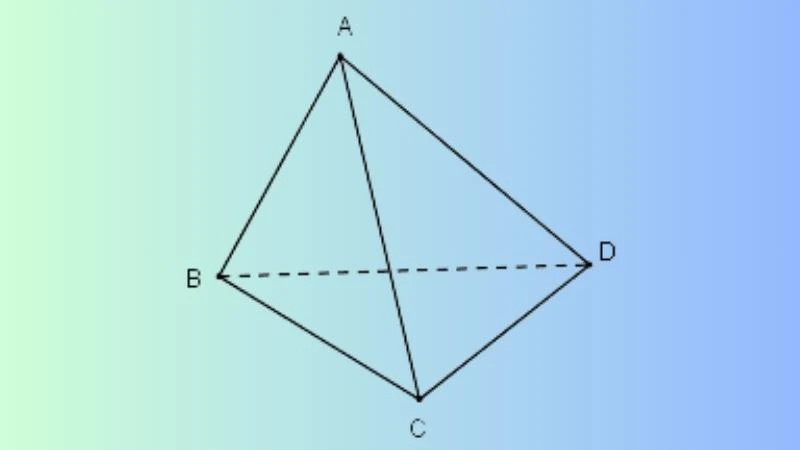
Phân Loại
Tứ diện đều là một trong năm loại khối đa diện đều. Những hình khối này có rất nhiều ứng dụng trong thực tế cũng như trong lý thuyết toán học.

Tính Chất Của Tứ Diện Đều
1. Các Tính Chất Nổi Bật
Tứ diện đều có những tính chất nổi bật như sau:
- Tất cả bốn mặt đều là các tam giác đều bằng nhau.
- Tổng các góc tại một đỉnh bất kì là 180 độ.
- Hai cặp cạnh đối diện có độ dài bằng nhau.
- Tâm của các mặt cầu nội tiếp và ngoại tiếp trùng nhau.
- Các đường cao của tứ diện đều có độ dài bằng nhau.
2. Các Hình Vẽ Minh Họa
Để hiểu rõ hơn về các tính chất của tứ diện đều, bạn có thể xem những hình ảnh dưới đây:
Cách Vẽ Tứ Diện Đều
Các Bước Vẽ Cụ Thể
Vẽ tứ diện đều là một bước quan trọng để giải quyết các bài toán hình học không gian. Để vẽ chính xác, bạn có thể thực hiện theo các bước sau:
- Bước 1: Xác định tứ diện đều là một hình chóp tam giác với đáy là tam giác BCD.
- Bước 2: Vẽ mặt đáy BCD trước tiên.
- Bước 3: Tìm trọng tâm G của tam giác BCD.
- Bước 4: Dựng đường vuông góc từ G lên đỉnh A của tứ diện đều.
- Bước 5: Nối các đỉnh để hoàn thiện hình tứ diện đều.
Công Thức Tính Thể Tích Khối Tứ Diện
Tính Thể Tích
Thể tích của khối tứ diện ABCD được tính bằng công thức:
\[ V = \frac{1}{3} \cdot S(BCD) \cdot AH \]
Trong đó:
- \( S(BCD) \) là diện tích của mặt đáy.
- \( AH \) là chiều cao của tứ diện từ đỉnh A tới mặt đáy BCD.
Đối Với Tứ Diện Đều
Công thức tính thể tích tứ diện đều với cạnh a sẽ là:
\[ V = \frac{a^3 \sqrt{2}}{12} \]
Bài Tập Tính Thể Tích Khối Tứ Diện
Bài Tập 1
Tính thể tích khối bài tập khối hộp ABCD.A’B’C’D’ biết rằng AA’B’D’ là khối tứ diện đều cạnh a.
Giải:
Do AA’A’D’ là tứ diện đều, từ đó bạn có thể xác định chiều cao và tính diện tích mặt đáy tương ứng để đạt được thể tích.
Bài Tập 2
Cho tứ diện ABCD gần đều, với các cặp cạnh đối bằng nhau: AB = CD = a, AC = BD = b và AD = BC = c. Hãy tính thể tích tứ diện ABCD.
Giải:
Bài tập này có thể được giải qua việc dựng tứ diện tương ứng và sử dụng công thức đã nêu trên để tính thể tích.
Kết Luận
Tứ diện và tứ diện đều là những khái niệm cần thiết trong hình học không gian, có thể áp dụng trong nhiều lĩnh vực khác nhau từ kiến thức lý thuyết đến ứng dụng thực tế. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn toàn diện về tứ diện.
Nếu bạn còn thắc mắc hay cần thêm thông tin, hãy để lại câu hỏi trong phần bình luận dưới đây! Chúc bạn học tốt!

















