Tam giác là một trong những hình dạng cơ bản trong hình học, và việc tính diện tích của nó là rất cần thiết trong nhiều ứng dụng khác nhau. Bài viết này sẽ hướng dẫn bạn cách tính diện tích tam giác với nhiều công thức khác nhau, từ tam giác thường, tam giác vuông, tam giác cân cho đến tam giác đều.
1. Tính Diện Tích Tam Giác Thường
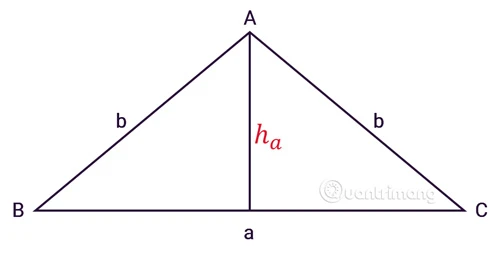
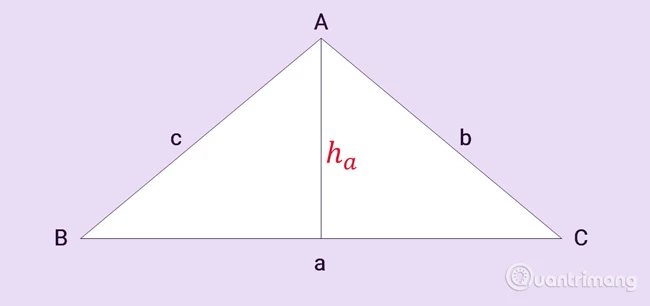
Tam giác thường có ba cạnh a, b, c. Giả sử ha là đường cao từ đỉnh A xuống cạnh BC (cạnh đối diện).
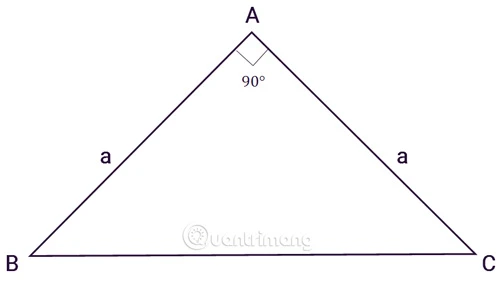
a. Công Thức Chung
Diện tích tam giác có thể được tính bằng:
\[ S = \frac{a \times h_a}{2} \]
Trong đó, \( S \) là diện tích, \( a \) là chiều dài của cạnh đáy, và \( h_a \) là chiều cao từ đỉnh A tới đáy.
Ví dụ minh họa:
Tính diện tích của tam giác có độ dài đáy là 5m và chiều cao là 24dm (2.4m).
Giải:
\[ S = \frac{5 \times 2.4}{2} = 6 \, m^2 \]
b. Tính Diện Tích Khi Biết Một Góc
Nếu biết hai cạnh kề và góc giữa chúng, diện tích can được tính bằng:
\[ S = \frac{1}{2} \times a \times b \times \sin(C) \]
Trong đó, C là góc giữa hai cạnh a và b.
Ví dụ nhanh:
Tam giác ABC có cạnh AB = 5, AC = 7 và góc A = 60 độ.
\[ S = \frac{1}{2} \times 5 \times 7 \times \sin(60°) \]
c. Tính Diện Tích Khi Biết 3 Cạnh
Khi biết độ dài ba cạnh, ta có thể sử dụng công thức Heron. Đầu tiên, tính nửa chu vi:
\[ p = \frac{a + b + c}{2} \]
Sau đó, diện tích được tính bằng:
\[ S = \sqrt{p(p-a)(p-b)(p-c)} \]
Ví dụ:
Với độ dài cạnh AB = 8, AC = 7, CB = 9.
\[ p = \frac{8 + 7 + 9}{2} = 12 \]
\[ S = \sqrt{12(12-8)(12-7)(12-9)} \]
d. Tính Diện Tích Bằng Bán Kính Đường Tròn Ngoại Tiếp
Nếu có bán kính R của đường tròn ngoại tiếp tam giác, diện tích được tính bằng:
\[ S = \frac{abc}{4R} \]
e. Tính Diện Tích Bằng Bán Kính Đường Tròn Nội Tiếp
Sử dụng công thức:
\[ S = p \times r \]
trong đó p là nửa chu vi, và r là bán kính đường tròn nội tiếp.
2. Tính Diện Tích Tam Giác Cân
Tam giác cân có hai cạnh bằng nhau (a), và độ dài cạnh đáy là b.
Công Thức
Diện tích tam giác cân là:
\[ S = \frac{b \times h}{2} \]
3. Tính Diện Tích Tam Giác Đều
Tam giác đều là loại tam giác có ba cạnh bằng nhau. Gọi a là độ dài cạnh của tam giác đều, diện tích dược tính bằng:
\[ S = \frac{a^2 \sqrt{3}}{4} \]
4. Tính Diện Tích Tam Giác Vuông
Tam giác vuông có một góc vuông. Gọi a và b là độ dài hai cạnh góc vuông. Diện tích được tính bằng:
\[ S = \frac{a \times b}{2} \]
Ví dụ minh họa:
Nếu a = 6, b = 8, thì:
\[ S = \frac{6 \times 8}{2} = 24 \]
5. Tính Diện Tích Tam Giác Vuông Cân
Tam giác vuông cân có hai cạnh góc vuông bằng nhau.
Công Thức
Nếu hai cạnh này đều có độ dài a:
\[ S = \frac{a^2}{2} \]
6. Công Thức Tính Diện Tích Tam Giác Trong Hệ Tọa Độ Oxyz
Trong không gian ba chiều, diện tích tam giác ABC có tọa độ ba đỉnh A(x1, y1, z1), B(x2, y2, z2), và C(x3, y3, z3) tính bằng công thức nhiên tích có hướng:
\[ S_{\triangle ABC} = \frac{1}{2} |\overrightarrow{AB} \wedge \overrightarrow{AC}| \]
Ví dụ:
Cho tam giác ABC có A(-1,1,2), B(1,2,3), C(3,-2,0). Ta có thể tính diện tích như sau.
Các Loại Tam Giác
- Tam giác thường: Cạnh và góc khác nhau.
- Tam giác cân: Hai cạnh bằng nhau.
- Tam giác đều: Tất cả ba cạnh bằng nhau với ba góc bằng nhau.
- Tam giác vuông: Một góc bằng 90 độ.
- Tam giác tù: Một góc lớn hơn 90 độ.
- Tam giác nhọn: Tất cả ba góc nhỏ hơn 90 độ.
Kết Luận
Tóm lại, việc tính diện tích tam giác rất quan trọng trong hình học, và việc áp dụng đúng công thức sẽ giúp bạn giải quyết các bài toán toán học một cách dễ dàng và hiệu quả. Hy vọng bài viết này sẽ giúp bạn có thêm kiến thức và áp dụng vào thực tiễn một cách tốt nhất. Nếu có bất kỳ thắc mắc nào, hãy để lại câu hỏi ở phần bình luận để được giải đáp!

















