Trong toán học, tam giác không chỉ là một trong những hình học cơ bản mà còn là chủ đề rất gần gũi với đời sống xung quanh chúng ta. Tính chu vi hình tam giác là một kiến thức nền tảng, giúp học sinh có thể phát triển những kỹ năng toán học cần thiết. Bài viết này sẽ khám phá các loại hình tam giác, cách tính chu vi của chúng và những ví dụ minh họa thực tế.
1. Tổng quan về hình tam giác
1.1 Định nghĩa hình tam giác
Hình tam giác là một hình phẳng có ba cạnh và ba đỉnh. Tam giác được phân loại dựa trên độ dài của các cạnh và các góc của nó:
- Tam giác thường: Có ba cạnh có độ dài khác nhau.
- Tam giác cân: Có hai cạnh bằng nhau.
- Tam giác vuông: Có một góc vuông (90 độ).
- Tam giác đều: Có ba cạnh bằng nhau.
1.2 Ý nghĩa của việc tính chu vi tam giác
Chu vi của tam giác giúp chúng ta hiểu tổng chiều dài của các cạnh, một thông số quan trọng trong nhiều ứng dụng thực tế, từ thiết kế kỹ thuật đến xây dựng.
2. Công thức tính chu vi hình tam giác
2.1 Tính chu vi tam giác thường
Tam giác thường là loại tam giác cơ bản có các cạnh không bằng nhau. Để tính chu vi, bạn áp dụng công thức:
Công thức: \( P = a + b + c \)
- P: Chu vi tam giác
- a, b, c: Độ dài các cạnh
Ví dụ: Cho tam giác có ba cạnh lần lượt là 4 cm, 6 cm và 7 cm.
Giải:
\[ P = 4 + 6 + 7 = 17 \text{ cm} \]
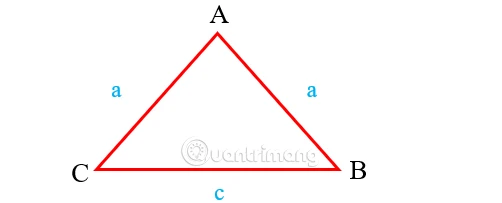
2.2 Chu vi hình tam giác cân
Tam giác cân có hai cạnh bằng nhau. Để tính chu vi, sử dụng công thức:
Công thức: \( P = 2a + b \)
- a: Độ dài của 2 cạnh bằng nhau
- b: Độ dài cạnh đáy
Ví dụ: Tính chu vi tam giác cân với hai cạnh bằng 5 cm và cạnh đáy 8 cm.
Giải:
\[ P = 2 \times 5 + 8 = 18 \text{ cm} \]
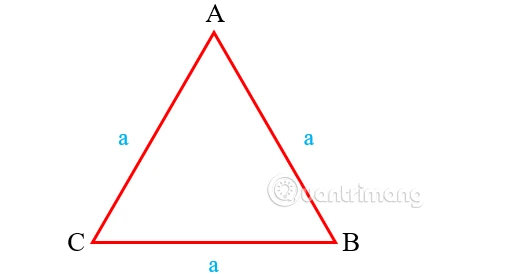
2.3 Chu vi hình tam giác đều
Tam giác đều có ba cạnh bằng nhau. Công thức tính chu vi như sau:
Công thức: \( P = 3 \times a \)
Ví dụ: Tính chu vi tam giác đều với cạnh dài 6 cm.
Giải:
\[ P = 3 \times 6 = 18 \text{ cm} \]
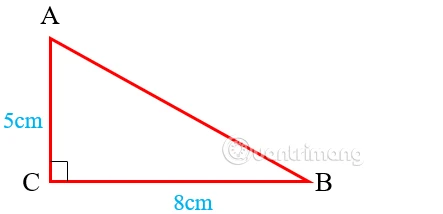
2.4 Chu vi hình tam giác vuông
Tam giác vuông có một góc vuông. Công thức tính chu vi là:
Công thức: \( P = a + b + c \)
- a, b: Các cạnh góc vuông
- c: Cạnh huyền
Ví dụ: Tính chu vi tam giác vuông với cạnh CA = 3 cm, CB = 4 cm và AB = 5 cm.
Giải:
\[ P = 3 + 4 + 5 = 12 \text{ cm} \]
3. Cách giải quyết các bài toán liên quan đến chu vi tam giác
3.1 Bài toán thực tế
Giả sử bạn có thể tính chu vi của một tam giác trong một bài toán thực tế. Hãy xem xét một ví dụ đơn giản:
Bài toán: Một mảnh đất có hình tam giác với các cạnh lần lượt là 7 m, 10 m và 5 m. Tính chu vi của mảnh đất đó.
Giải:
\[ P = 7 + 10 + 5 = 22 \text{ m} \]
3.2 Bài toán trong không gian
Khi bạn cần tính chu vi tam giác trong không gian, việc sử dụng tọa độ là rất quan trọng.
Bài toán: Trong không gian có hai điểm A(1, 2), B(4, 5) và điểm C(2, 1). Tính chu vi tam giác ABC.
Giải:
- Tính độ dài các cạnh bằng công thức khoảng cách giữa hai điểm:
\[
AB = \sqrt{(4-1)^2 + (5-2)^2} = \sqrt{9 + 9} = \sqrt{18} \approx 4.24
\]
\[
BC = \sqrt{(4-2)^2 + (5-1)^2} = \sqrt{4 + 16} = \sqrt{20} \approx 4.47
\]
\[
CA = \sqrt{(2-1)^2 + (1-2)^2} = \sqrt{1 + 1} = \sqrt{2} \approx 1.41
\]
\[
P = AB + BC + CA \approx 4.24 + 4.47 + 1.41 \approx 10.12
\]
4. Tóm tắt các loại tam giác và công thức tính chu vi
4.1 Bảng tổng hợp
| Loại tam giác | Công thức chu vi |
|-------------------|---------------------|
| Tam giác thường | \( P = a + b + c \) |
| Tam giác cân | \( P = 2a + b \) |
| Tam giác đều | \( P = 3a \) |
| Tam giác vuông | \( P = a + b + c \) |
4.2 Kết luận
Việc tính chu vi hình tam giác không chỉ là một bài học toán học lý thuyết mà còn có ứng dụng thực tiễn đáng kể trong nhiều lĩnh vực. Hiểu rõ các loại tam giác và các công thức tính chu vi giúp bạn tự tin hơn trong việc giải quyết các bài toán từ đơn giản đến phức tạp.
Hãy thường xuyên luyện tập và thử thách bản thân với những bài toán khác nhau để cải thiện kỹ năng của mình trong lĩnh vực này!















