Hình tứ giác là một trong những chủ đề cơ bản và quan trọng trong toán học. Đặc biệt, tứ giác lồi là một khái niệm thú vị mà học sinh cần nắm vững trong quá trình học tập. Hãy cùng khám phá kiến thức đầy đủ về tứ giác lồi cũng như công thức và ứng dụng của nó.
Định Nghĩa Tứ Giác Lồi
Khái Niệm Cơ Bản
Tứ giác lồi là một loại đa giác có 4 đỉnh và 4 cạnh, trong đó không có bất kỳ 2 đoạn thẳng nào nằm trên cùng một đường thẳng. Thông thường, tứ giác lồi có các tính chất cụ thể như tổng các góc trong là 360 độ.
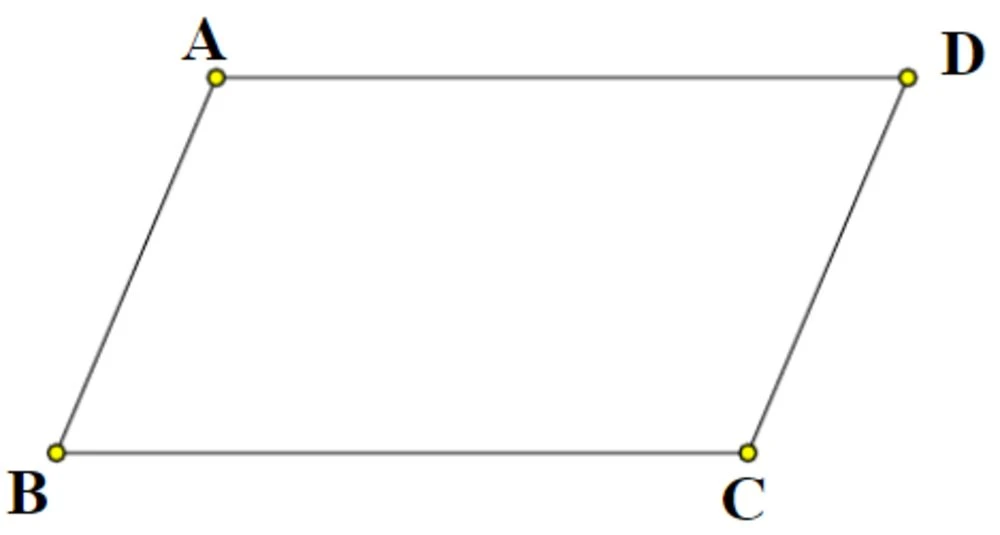
- Kí hiệu: Trong các bài toán, tứ giác lồi thường được ký hiệu là ABCD.
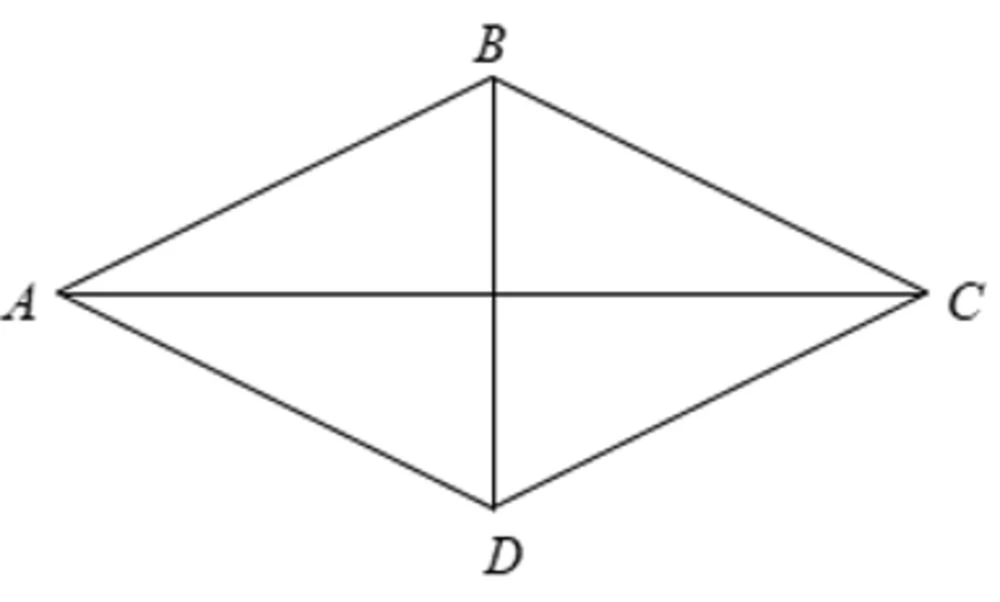
- Tính chất: Tứ giác lồi có các đường chéo cắt nhau tại điểm nằm bên trong tứ giác.

Phân Loại Tứ Giác Lồi
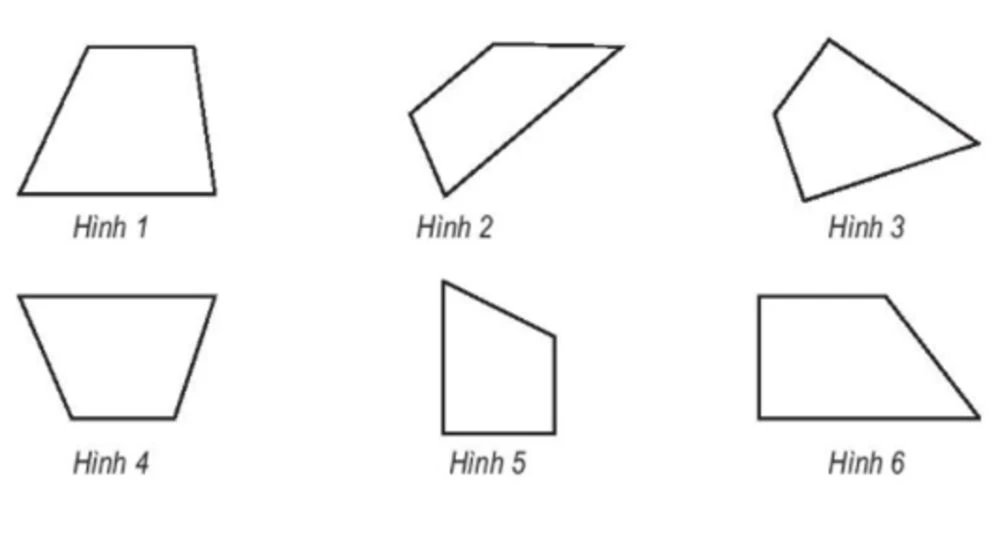
Tứ giác có thể được phân loại thành các loại đơn giản hoặc phức tạp. Dưới đây là phân loại chính của tứ giác:
- Tứ giác đơn: Không có cạnh nào cắt nhau.
- Tứ giác lõm: Có ít nhất một góc lớn hơn 180 độ.
- Tứ giác lồi: Tất cả các góc đều nhỏ hơn 180 độ.

Tính Chất Của Tứ Giác Lồi
Tính Chất Về Góc
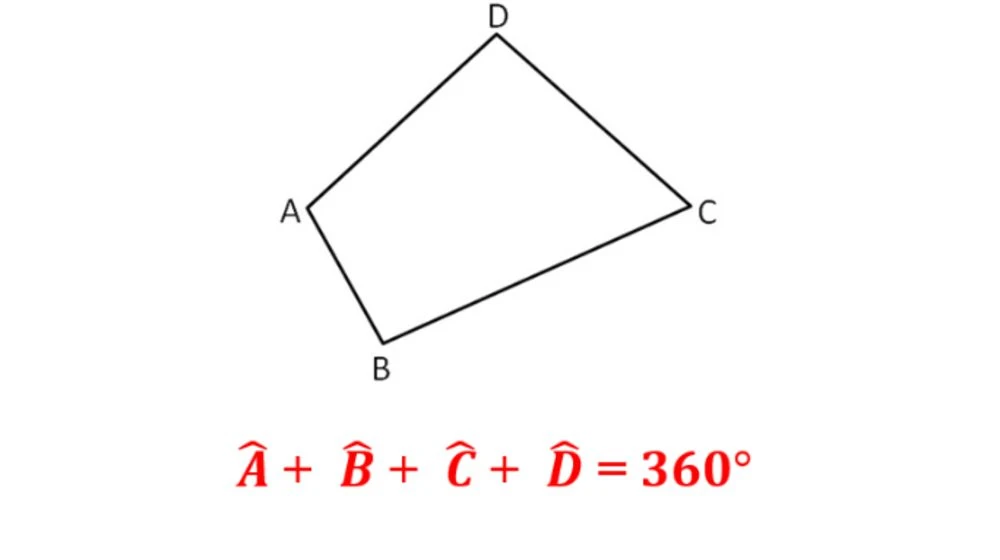
Tổng các góc trong của hình tứ giác lồi là 360 độ. Điều này có ý nghĩa quan trọng trong thiết kế và ứng dụng hình học.
Tính Chất Về Đường Chéo
Trong một tứ giác lồi, hai đường chéo của nó luôn cắt nhau tại một điểm nằm trong miền của tứ giác. Điều này tạo nên một số tính chất chuyển tiếp liên quan đến các phần diện tích do đường chéo chia thành.
Các Dạng Hình Tứ Giác Đặc Biệt
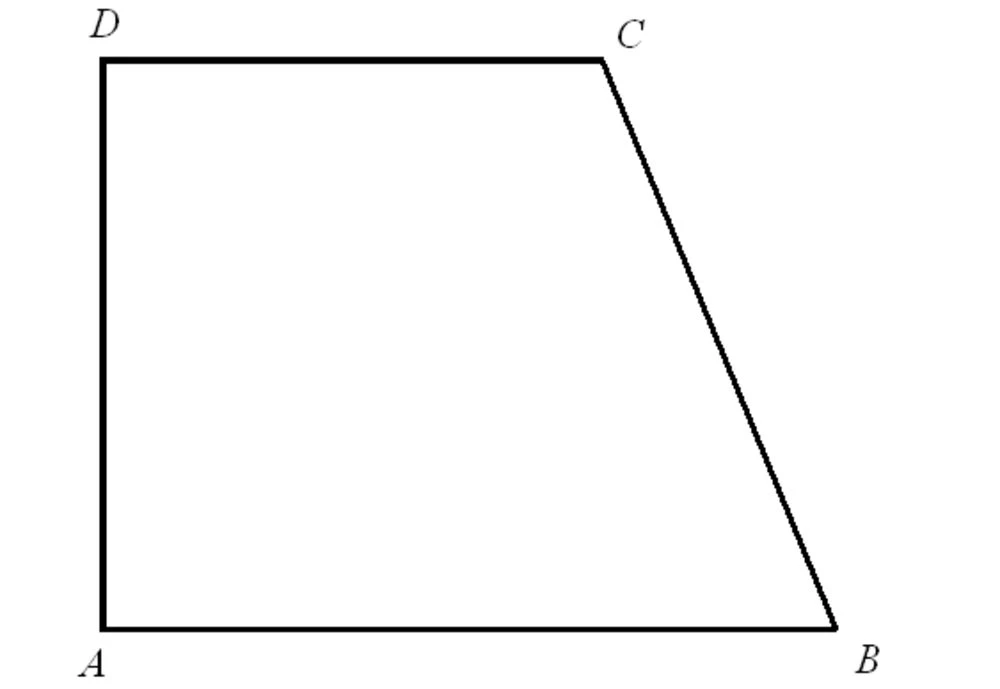
1. Hình Thang
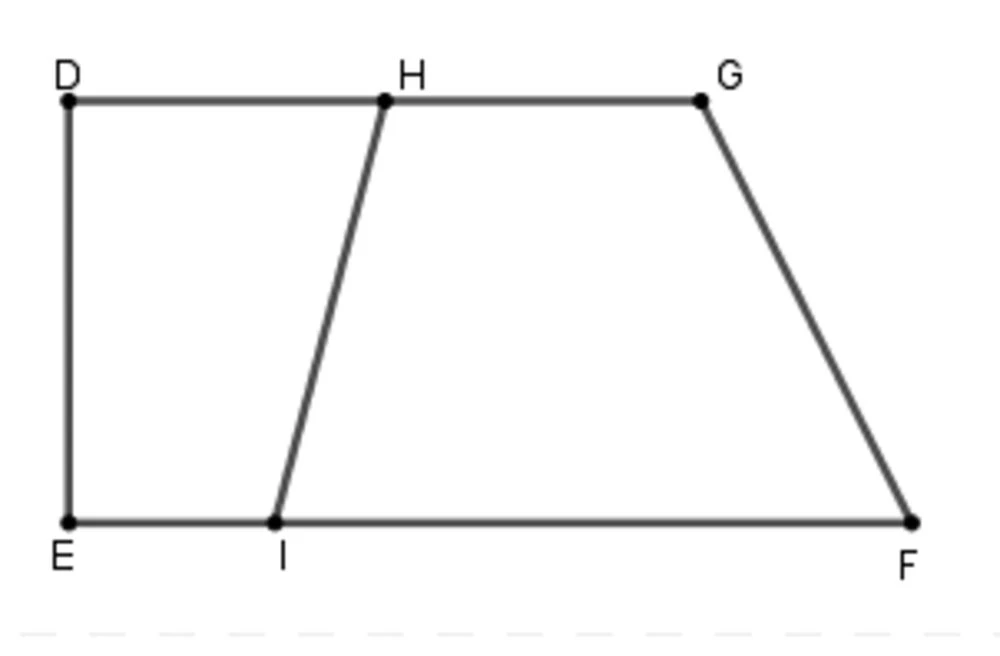
Hình thang là một dạng tứ giác mà có ít nhất một cặp cạnh đối song song. Điều này làm cho hình thang có các tính chất độc đáo liên quan đến góc và đường chéo.
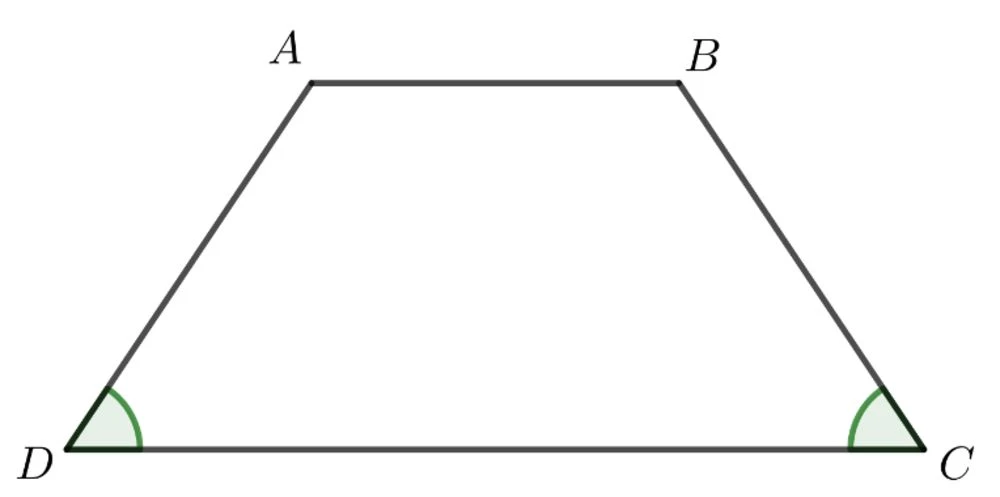
2. Hình Thang Cân
Là hình thang mà không chỉ có một cặp cạnh đối song song mà còn hai góc kề ở một cạnh đáy bằng nhau. Hình thang cân có tính đối xứng đặc biệt.

3. Hình Bình Hành
Hình bình hành là trường hợp tứ giác có hai cặp cạnh đối song song, các góc đối bằng nhau, và hai đường chéo cắt nhau tại trung điểm mỗi đường.
4. Hình Thoi
Hình thoi là tứ giác có tất cả 4 cạnh bằng nhau. Điều này có nghĩa rằng các góc trong của nó không giống nhau nhưng lại có một số tính chất tương tự với hình bình hành.
5. Hình Chữ Nhật
Hình chữ nhật là tứ giác có 4 góc vuông. Do đó, đường chéo của hình chữ nhật không chỉ bằng nhau mà còn cắt nhau tại trung điểm của từng đoạn.
6. Hình Vuông
Hình vuông là tứ giác đặc biệt nhất với tất cả các cạnh bằng nhau và tất cả các góc vuông. Hình vuông vừa là hình chữ nhật vừa là hình thoi.
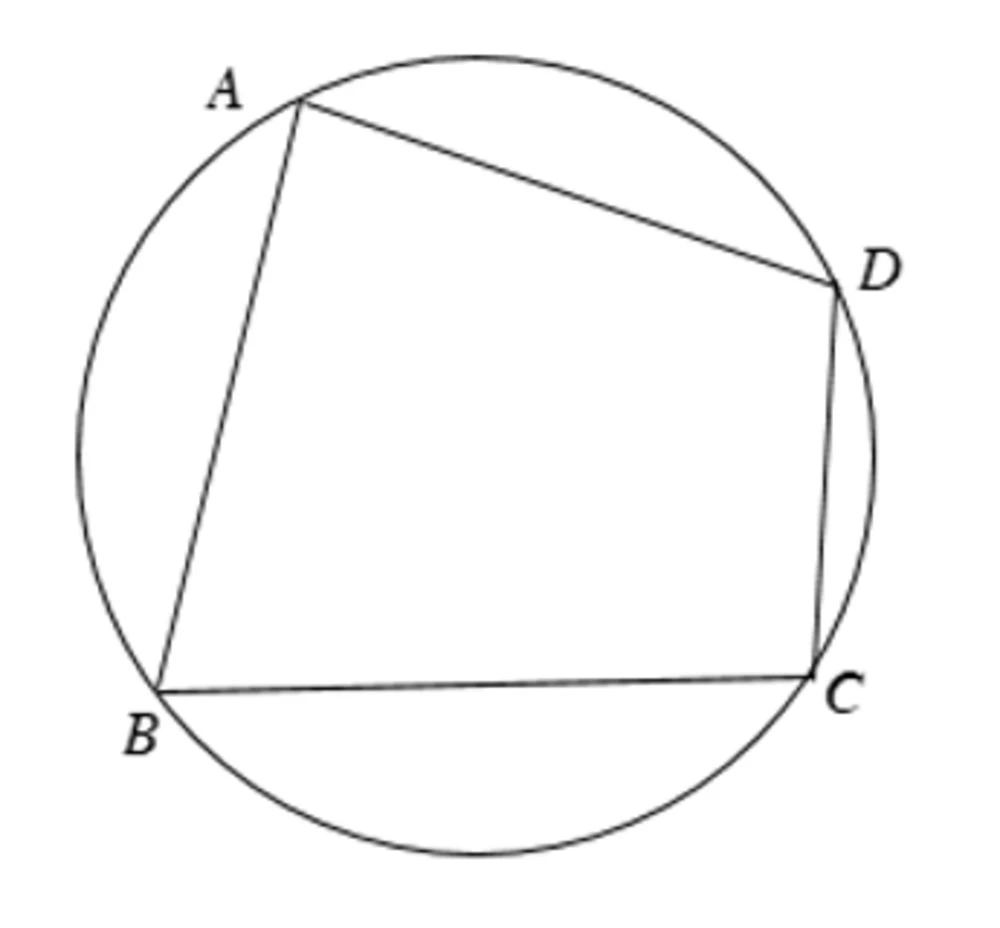
7. Tứ Giác Nội Tiếp
Tứ giác nội tiếp là hình tứ giác có bốn đỉnh nằm trên cùng một đường tròn.
Công Thức Tính Chu Vi và Diện Tích Tứ Giác
Công Thức Chu Vi Tứ Giác
Chu vi của tứ giác được tính bằng tổng chiều dài tất cả các cạnh. Công thức tính chu vi như sau:
\[ P = a + b + c + d \]
Trong đó:
- \( P \): Chu vi tứ giác
- \( a, b, c, d \): chiều dài của các cạnh
Công Thức Diện Tích Tứ Giác
Diện tích tứ giác không có một công thức chung mà phụ thuộc vào loại tứ giác cụ thể. Ví dụ:
- Diện tích hình vuông: \( S = a \times a \)
- Diện tích hình chữ nhật: \( S = a \times b \)
- Diện tích hình bình hành: \( S = a \times h \) (với \( h \) là chiều cao)
Bài Tập Luyện Tập
Để nắm vững kiến thức về tứ giác lồi, hãy luyện tập với một số bài tập dưới đây.
Bài Tập 1: Tính Chu Vi
Cho tứ giác ABCD có các cạnh như sau:
- AB = 5 cm
- BC = 7 cm
- CD = 9 cm
- DA = 5 cm
Tính chu vi của hình tứ giác ABCD.
Bài Tập 2: Tính Diện Tích
Cho hình chữ nhật có chiều dài là 8 cm và chiều rộng là 6 cm. Hãy tính diện tích của hình chữ nhật.
Bài Tập 3: Tính Tổng Các Góc
Một hình tứ giác có tổng số đo các góc là 360 độ. Nếu góc A = 90 độ, góc B = 80 độ, hãy tính góc C và góc D.
Bí Quyết Ghi Nhớ Kiến Thức Về Tứ Giác
Để ghi nhớ hiệu quả các kiến thức về hình tứ giác, học sinh cần:
- Học Và Thực Hành: Thực hành qua nhiều bài tập giúp nhớ lâu hơn.
- Sử Dụng Hình Ảnh Trực Quan: Hình dung các loại tứ giác, kèm theo sơ đồ.
- Chơi Trò Chơi Học Tập: Sử dụng các app học toán để tăng cường sự hứng thú.
Kết Luận
Tìm hiểu kiến thức về tứ giác lồi không chỉ giúp học sinh nắm chắc kiến thức toán học mà còn phát triển tư duy logic. Hy vọng rằng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan về tứ giác lồi cùng với các ứng dụng thực tiễn trong đời sống. Việc ghi nhớ và thực hành các công thức, tính chất sẽ giúp bạn tự tin hơn trong học tập và các kỳ thi.
























