Hình học là một lĩnh vực quan trọng trong toán học, với nhiều ứng dụng trong thực tiễn và trong việc phát triển tư duy logic của học sinh. Trong số các khối hình học, khối lập phương là một trong những dạng cơ bản nhất mà học sinh thường gặp trong chương trình học từ cấp 1 đến cấp 3. Bài viết này sẽ đi sâu vào việc tìm hiểu công thức tính thể tích hình lập phương, hướng dẫn giải bài toán và một số bài tập thực hành để củng cố kiến thức cho học sinh lớp 5.
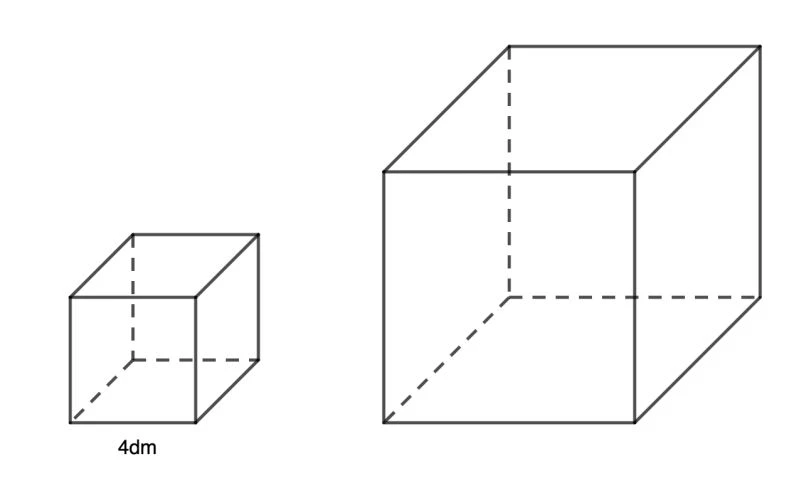
1. Khái niệm cơ bản về hình lập phương
Hình lập phương là một khối hình có các đặc điểm sau:
- Có 6 mặt phẳng, tất cả đều là hình vuông và diện tích của các mặt bằng nhau.
- Có 12 cạnh, tất cả đều bằng nhau.
- Có 8 đỉnh, mỗi đỉnh là điểm giao nhau của ba cạnh.
- Đường chéo của tất cả các mặt đều bằng nhau và được tính theo công thức.
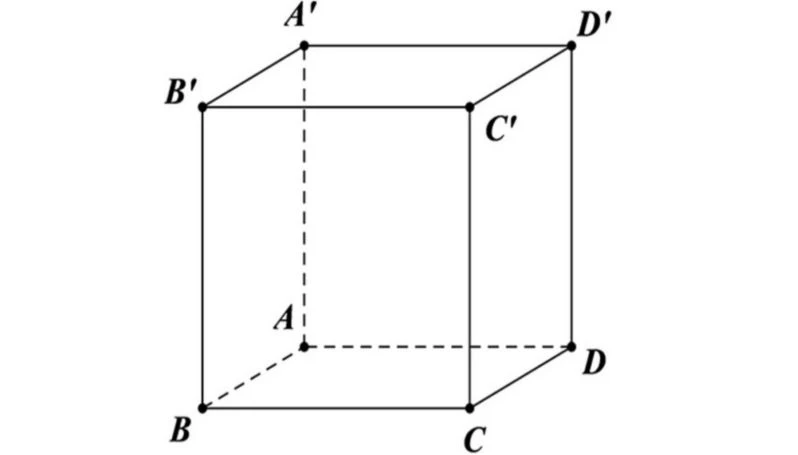
1.1. Tính chất của hình lập phương
Hình lập phương có những tính chất đáng chú ý dưới đây:
- Mỗi mặt đều có diện tích bằng nhau.
- Là khối lượng có chiều cao, chiều rộng và chiều dài bằng nhau.
- Cạnh hình lập phương được ký hiệu là \(a\).
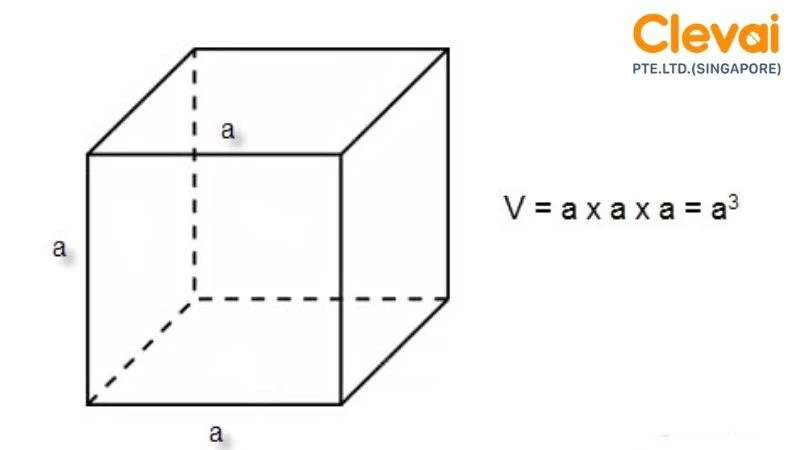
2. Công thức tính thể tích hình lập phương
2.1. Công thức tổng quát
Để tính thể tích \(V\) của hình lập phương, bạn có thể sử dụng công thức đơn giản như sau:
\[
V = a \times a \times a = a^3
\]
Trong đó:
- V là thể tích.
- a là độ dài cạnh của hình lập phương.
2.2. Ví dụ minh họa
Ví dụ 1:
Giả sử bạn có một hình lập phương với cạnh dài \(a = 4\) cm.
\[
V = 4 \times 4 \times 4 = 64 \text{ cm}^3
\]
Điều này có nghĩa là thể tích khối hình lập phương đó là 64 cm³.
3. Hướng dẫn giải bài toán liên quan đến thể tích hình lập phương
Để giải bài toán liên quan đến thể tích hình lập phương, bạn cần nắm rõ các dạng bài sau:
3.1. Dạng 1: Tính thể tích khi biết độ dài cạnh
Trong trường hợp này, chỉ cần áp dụng định nghĩa đã nêu ở trên.
3.2. Dạng 2: Tính thể tích khi biết diện tích một mặt
- Tính diện tích của một mặt hình lập phương (diện tích \(S\)):
\[
S = a^2
\]
- Từ đó, tính cạnh của hình lập phương:
\[
a = \sqrt{S}
\]
- Tiếp theo, sử dụng công thức tính thể tích.
3.3. Dạng 3: Tính độ dài cạnh khi biết thể tích
Nếu công thức thể tích đã biết, bạn có thể tính được độ dài cạnh bằng công thức đảo ngược:
\[
a = \sqrt[3]{V}
\]
3.4. Dạng 4: So sánh thể tích giữa các hình lập phương
Khi được yêu cầu so sánh thể tích giữa các hình lập phương khác nhau, chỉ cần tính thể tích từng hình và so sánh kết quả.
3.5. Dạng 5: Toán có lời văn
Trong toán học, việc phân tích đề bài và áp dụng kiến thức là rất quan trọng. Đọc kỹ đề và xác định dạng toán là cần thiết để giải quyết vấn đề hiệu quả.
4. Một số bài toán mẫu
Bài 1: Tính thể tích khối lập phương có cạnh bằng 3 cm.
Giải:
\[
V = 3 \times 3 \times 3 = 27 \text{ cm}^3
\]
Đáp số: 27 cm³
Bài 2: Tính khối lượng của một khối kim loại hình lập phương có cạnh là 5 m, biết mỗi dm³ kim loại nặng 10 kg.
Giải:
- Tính thể tích khối kim loại:
\[
V = 5 \times 5 \times 5 = 125 \text{ m}^3
\]
- Đổi sang dm³ (1 m³ = 1000 dm³):
\[
V = 125 \times 1000 = 125000 \text{ dm}^3
\]
\[
Khối lượng = 10 \times 125000 = 1250000 \text{ kg}
\]
Đáp số: 1250000 kg
Bài 3: Tính thể tích khối lập phương B gấp đôi cạnh của khối lập phương A có cạnh 4 cm.
Giải:
- Cạnh của khối lập phương B:
\[
Cạnh_B = 4 \times 2 = 8 \text{ cm}
\]
- Tính thể tích hình lập phương B:
\[
V_B = 8 \times 8 \times 8 = 512 \text{ cm}^3
\]
- Tính thể tích hình lập phương A:
\[
V_A = 4 \times 4 \times 4 = 64 \text{ cm}^3
\]
\[
\frac{V_B}{V_A} = \frac{512}{64} = 8
\]
Thể tích của B gấp 8 lần thể tích của A.
5. Kết luận
Qua bài viết này, bạn đã nắm rõ về khái niệm, công thức tính và ứng dụng của thể tích hình lập phương trong các bài toán. Thể tích hình lập phương không chỉ là kiến thức lý thuyết mà còn là một trong những kỹ năng cần thiết giúp học sinh phát triển tư duy và khả năng giải quyết vấn đề trong môn học toán. Hy vọng rằng những thông tin và bài toán mẫu mà Clevai cung cấp sẽ hữu ích cho bạn trong quá trình học tập và ôn luyện.















