1. Giới thiệu về thể tích hình trụ
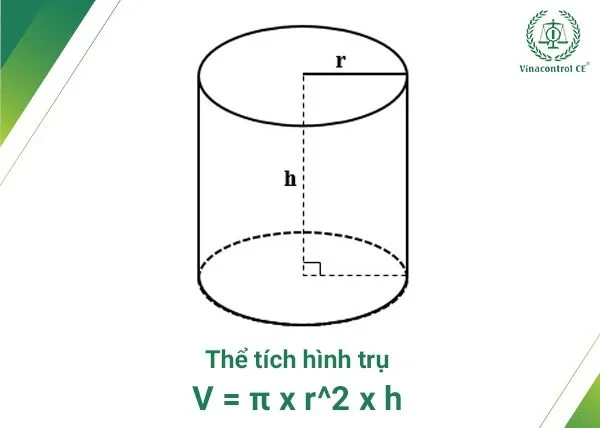
Thể tích hình trụ là một khái niệm cơ bản trong toán học, đặc biệt là trong hình học không gian. Hình trụ được định nghĩa là khối có hai đáy là hai mặt tròn bằng nhau và song song, với các điểm ở đáy được nối với nhau thông qua các đường thẳng. Để tính thể tích của hình trụ, công thức chính xác là:
Công thức:
\[ V = \pi r^2 h \]
Trong đó:
- \( V \): thể tích của hình trụ (đơn vị: cm³)
- \( r \): bán kính đáy (đơn vị: cm)
- \( h \): chiều cao của hình trụ (đơn vị: cm)
- \( \pi \): hằng số Pi (~3.14)
1.1 Ý nghĩa của công thức
Công thức tính thể tích hình trụ thể hiện rằng thể tích phụ thuộc vào diện tích mặt đáy và chiều cao của hình trụ. Diện tích mặt đáy được tính bằng công thức \( S = \pi r^2 \), do đó, thể tích hình trụ có thể hiểu là tích của diện tích mặt đáy và chiều cao.
2. Các bước giải bài tập tính thể tích hình trụ
Có nhiều dạng bài tập khác nhau liên quan đến việc tính thể tích hình trụ. Dưới đây là hướng dẫn cụ thể để giải các dạng bài tập từ cơ bản đến nâng cao.
2.1 Tính thể tích hình trụ biết bán kính và chiều cao
Ví dụ 1:
Tính thể tích hình trụ biết bán kính đáy bằng 3 cm và chiều cao bằng 10 cm.
Giải:
- Bán kính \( r = 3 \) cm
- Chiều cao \( h = 10 \) cm
Áp dụng công thức:
\[ V = \pi \cdot r^2 \cdot h = \pi \cdot (3^2) \cdot 10 = 90\pi \approx 282.74 \text{ cm}^3 \]
Kết luận: Thể tích hình trụ là 90π cm³ (khoảng 282.74 cm³).
2.2 Tìm chiều cao khi biết thể tích và bán kính
Ví dụ 2:
Một hình trụ có thể tích 150 cm³ và bán kính đáy là 5 cm. Tính chiều cao của hình trụ.
Giải:
Áp dụng công thức:
\[ V = \pi r^2 h \]
=>
\[ 150 = \pi \cdot (5^2) \cdot h \]
=>
\[ 150 = 25\pi h \]
=>
\[ h = \frac{150}{25\pi} = \frac{6}{\pi} \approx 1.91 \text{ cm} \]
Kết luận: Chiều cao của hình trụ là khoảng 1.91 cm.
2.3 Tìm bán kính khi biết thể tích và chiều cao
Ví dụ 3:
Cho một hình trụ có thể tích 200 cm³ và chiều cao 10 cm. Tính bán kính đáy.
Giải:
Áp dụng công thức:
\[ V = \pi r^2 h \]
=>
\[ 200 = \pi r^2 \cdot 10 \]
=>
\[ r^2 = \frac{200}{10\pi} = \frac{20}{\pi} \]
=>
\[ r = \sqrt{\frac{20}{\pi}} \approx 2.52 \text{ cm} \]
Kết luận: Bán kính đáy của hình trụ là khoảng 2.52 cm.
3. Các dạng bài tập nâng cao
Để có được kiến thức sâu hơn, chúng ta có thể giải quyết một số bài tập nâng cao liên quan đến hình trụ tương tác với nhiều khối hình khác nhau.
3.1 Tính thể tích khi hình trụ cắt nhau
Ví dụ 4:
Hai hình trụ có chiều cao lần lượt là 10 cm và 15 cm, bán kính đáy đều là 3 cm. Tính thể tích phần giao nhau của hai hình trụ.
Giải:
Để tính thể tích giao nhau, ta cần áp dụng phương pháp lập mô hình thể tích và tìm thể tích hình trụ lớn hơn trừ đi thể tích hình trụ nhỏ hơn. Xét cả hai hình trụ có thể tính thể tích một cách riêng biệt.
Thể tích hình trụ 1:
\[ V_1 = \pi \cdot (3^2) \cdot 10 = 90\pi \]
Thể tích hình trụ 2:
\[ V_2 = \pi \cdot (3^2) \cdot 15 = 135\pi \]
Phần giao nhau có thể tính là diện tích chồng lên nhau:
\[ V_{giao} = \frac{10}{25}V_1 + \frac{15}{25}V_2 = 0.4V_1 + 0.6V_2 \]
Kết luận: Tính toán chi tiết hơn cần chọn hệ toạ độ và phương pháp giải riêng.
4. Kết luận
Tính thể tích hình trụ là một phần quan trọng của toán học và có rất nhiều ứng dụng trong ngành kiến trúc, công nghiệp và khảo sát đất đai. Bằng cách áp dụng công thức và các kỹ năng giải bài tập mà chúng ta đã đề cập, bạn có thể tự tin tính toán thể tích hình trụ trong nhiều bối cảnh khác nhau.
Hy vọng rằng bài viết này cung cấp cho bạn cái nhìn sâu sắc và đầy đủ về thể tích hình trụ, cũng như giúp bạn ứng dụng kiến thức này trong học tập và cuộc sống hàng ngày. Hãy tiếp tục thực hành và khám phá nhiều hơn về toán học để thuần thục những kỹ năng này!













