Khái niệm về kết quả của phép nhân
Khi chúng ta nhắc đến việc tính toán trong toán học, thuật ngữ thường xuất hiện đầu tiên chính là kết quả của phép nhân. Đó là một trong những khái niệm cơ bản và quan trọng trong lĩnh vực này. Kết quả này không chỉ đơn giản là con số, mà còn là một cách để chúng ta hiểu về mối quan hệ giữa các số với nhau.
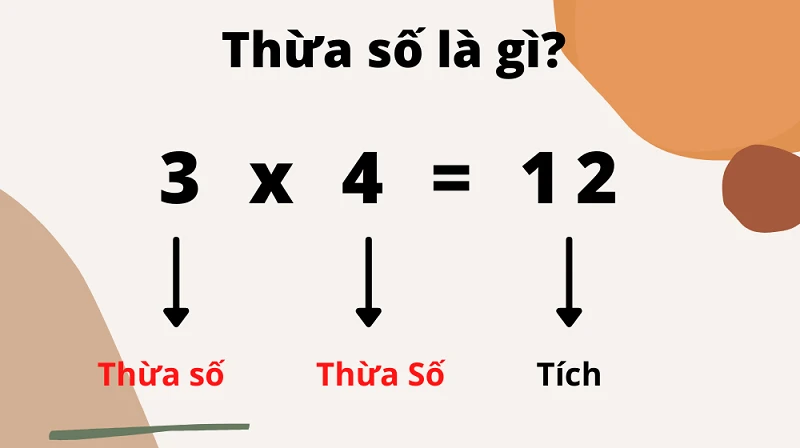
Khi thực hiện phép nhân giữa hai số, kết quả thu được được gọi là kết quả của phép nhân. Ví dụ, khi ta nhân số 2 với số 3, kết quả là 6. Trong trường hợp này, 2 và 3 được gọi là các số hạng hay thừa số, và 6 được gọi là kết quả hoặc tích.
Khái niệm này không chỉ giới hạn trong các phép tính đơn giản. Trong toán học, nó còn mở rộng ra nhiều lĩnh vực khác nhau, từ đại số đến hình học, và thậm chí là các lĩnh vực khoa học khác. Khi hiểu rõ về tích, chúng ta có thể áp dụng nó để giải quyết các bài toán phức tạp và phát triển tư duy logic.
Các loại tích và ứng dụng trong đời sống
Có nhiều loại tích khác nhau mà chúng ta có thể gặp trong toán học, mỗi loại có những đặc điểm và ứng dụng riêng. Một số loại tích phổ biến bao gồm:
Tích số
Tích số là một thuật ngữ dùng để chỉ kết quả của phép nhân giữa hai hoặc nhiều số. Ví dụ: khi nhân 4 với 5, kết quả là 20, và ta có thể nói rằng 20 là tích số của 4 và 5. Tích số được ứng dụng trong rất nhiều lĩnh vực khác nhau, từ tính toán giá trị trong kinh doanh đến các bài toán khoa học.
Tích vô hướng và tích có hướng
Trong hình học và đại số, tích được chia thành tích vô hướng và tích có hướng. Tích vô hướng thường được sử dụng để tính toán diện tích hoặc thể tích, trong khi tích có hướng thường liên quan đến các khái niệm như lực hoặc vận tốc.
Tích phân
Tích phân là một khái niệm quan trọng trong giải tích, được sử dụng để tính toán các đại lượng như diện tích dưới đường cong hoặc thể tích của hình khối. Đây là một lĩnh vực phức tạp nhưng rất quan trọng trong khoa học và kỹ thuật.
Tích có vai trò rất quan trọng trong đời sống hàng ngày. Chúng ta có thể thấy ứng dụng của nó trong việc tính toán giá cả, chi phí sản xuất, hay thậm chí trong việc lập kế hoạch ngân sách cá nhân.
Các tính chất của phép nhân
Trong toán học, phép nhân có những tính chất đặc trưng mà chúng ta cần nắm rõ để thực hiện các phép tính một cách chính xác và hiệu quả. Dưới đây là một số tính chất cơ bản của phép nhân:
Tính giao hoán
Tính giao hoán của phép nhân có nghĩa là thứ tự của các số hạng không ảnh hưởng đến kết quả. Ví dụ, 2 x 3 = 3 x 2, cả hai phép tính đều cho kết quả là 6. Tính chất này rất hữu ích trong việc sắp xếp và thực hiện các phép tính phức tạp hơn.
Tính kết hợp
Tính kết hợp cho phép chúng ta nhóm các số hạng lại với nhau theo nhiều cách khác nhau. Ví dụ, (2 x 3) x 4 = 2 x (3 x 4). Cả hai cách nhóm đều cho kết quả là 24. Điều này giúp chúng ta dễ dàng tính toán khi làm việc với nhiều số hạng.
Tính phân phối
Tính phân phối cho phép chúng ta phân phối một số hạng ra nhiều số khác. Ví dụ, 2 x (3 + 4) = 2 x 3 + 2 x 4. Kết quả của cả hai phép tính đều là 14. Tính chất này đặc biệt quan trọng trong đại số, nơi chúng ta thường phải làm việc với các biểu thức phức tạp.
Những tính chất này không chỉ giúp cho việc tính toán trở nên dễ dàng hơn, mà còn giúp phát triển tư duy logic và khả năng giải quyết vấn đề.
Bài tập và cách tính tích
Để hiểu rõ hơn về khái niệm này, chúng ta có thể thực hành một số bài tập đơn giản. Dưới đây là một số ví dụ và cách tính tích mà bạn có thể tham khảo:
Bài tập 1: Tính tích của hai số
Câu hỏi: Tính tích của 7 và 8.
Giải: 7 x 8 = 56.
Bài tập 2: Tính tích với nhiều số
Câu hỏi: Tính tích của 2, 3 và 5.
Giải: (2 x 3) x 5 = 6 x 5 = 30.
Bài tập 3: Ứng dụng của tích
Câu hỏi: Nếu một chiếc xe tiêu thụ 5 lít xăng cho mỗi 100 km, hãy tính lượng xăng tiêu thụ cho 250 km.
Giải: 250 km = 2.5 x 100 km, do đó lượng xăng tiêu thụ là 2.5 x 5 = 12.5 lít.
Khi làm bài tập, bạn cần chú ý đến thứ tự thực hiện các phép tính và áp dụng các tính chất của phép nhân để đạt được kết quả chính xác nhất.
Kết luận
Kết quả của phép nhân là một khái niệm cơ bản nhưng rất quan trọng trong toán học và các lĩnh vực khác nhau trong cuộc sống. Việc nắm vững các loại tích, tính chất của phép nhân và cách tính tích sẽ giúp bạn giải quyết các bài toán phức tạp và phát triển khả năng tư duy logic.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về khái niệm này, và khuyến khích bạn áp dụng vào thực tế để nâng cao kỹ năng toán học của mình. Hãy luôn thực hành và khám phá thêm nhiều điều thú vị trong thế giới của các con số!
