Cách chứng minh trung điểm của đoạn thẳng trong hình học

Giới thiệu về khái niệm trung điểm

Trong toán học, đặc biệt là trong hình học, khái niệm trung điểm của một đoạn thẳng là một trong những khái niệm cơ bản nhưng lại rất quan trọng. Trung điểm của một đoạn thẳng được định nghĩa là điểm nằm giữa hai đầu của đoạn thẳng đó, với khoảng cách từ điểm này đến hai đầu đoạn thẳng là bằng nhau. Điều này có nghĩa là nếu ta có hai điểm A và C tạo thành đoạn thẳng AC, thì điểm B là trung điểm nếu nó thỏa mãn hai điều kiện: B nằm giữa A và C, và khoảng cách AB bằng với khoảng cách BC.

Các yếu tố cần thiết để chứng minh một điểm là trung điểm

Để chứng minh một điểm là trung điểm của một đoạn thẳng, có những yếu tố chính mà chúng ta cần chú ý:

• Điều kiện về vị trí: Điểm cần chứng minh phải nằm giữa hai điểm đầu của đoạn thẳng. Nếu A và C là hai điểm đầu của đoạn thẳng AC, thì điểm B cần phải thuộc đoạn thẳng AC.
• Điều kiện về độ dài: Khoảng cách từ điểm B đến hai điểm A và C phải bằng nhau. Cụ thể, ta phải chứng minh rằng AB = BC.

Nếu cả hai điều kiện trên đều được đáp ứng, lúc này ta có thể khẳng định rằng B là trung điểm của đoạn thẳng AC.

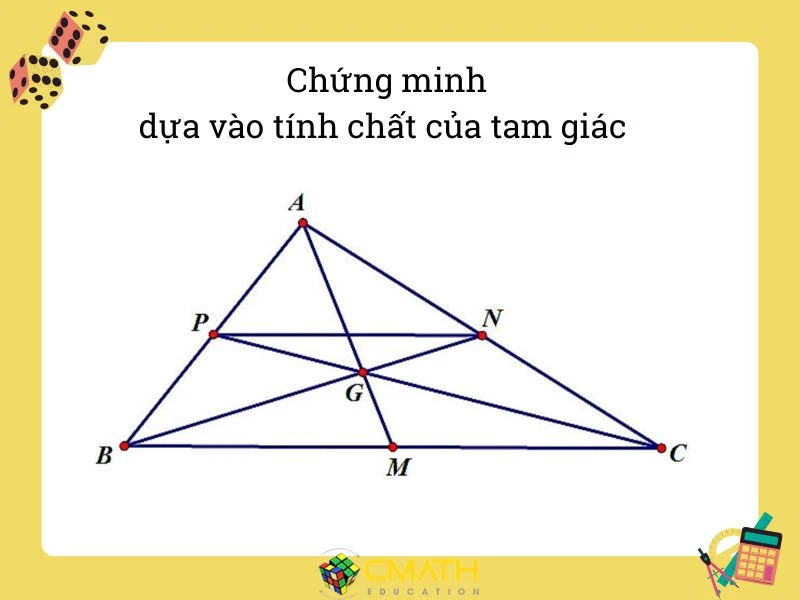
Cách chứng minh một điểm là trung điểm

Để thực hiện việc chứng minh, ta thường áp dụng một số phương pháp nhất định. Sau đây là các bước cơ bản để chứng minh một điểm là trung điểm của đoạn thẳng:

Bước 1: Xác định vị trí

Trước tiên, ta cần chứng minh rằng điểm B nằm giữa hai điểm A và C. Cách làm này có thể thực hiện bằng việc sử dụng các định nghĩa liên quan đến đường thẳng và đoạn thẳng trong hình học. Ta có thể sử dụng tọa độ của các điểm A, B, C để kiểm tra xem liệu B có nằm giữa A và C hay không.

Bước 2: Chứng minh độ dài hai đoạn thẳng bằng nhau

Tiếp theo, ta cần chứng minh rằng độ dài của đoạn AB bằng độ dài của đoạn BC. Để làm điều này, ta có thể áp dụng định lý khoảng cách trong mặt phẳng tọa độ. Nếu A có tọa độ (x1, y1), B có tọa độ (x2, y2), và C có tọa độ (x3, y3), ta có thể tính độ dài của các đoạn thẳng như sau:

• Độ dài AB = √((x2 - x1)² + (y2 - y1)²)
• Độ dài BC = √((x3 - x2)² + (y3 - y2)²)

Sau khi tính toán, nếu ta tìm thấy độ dài AB = BC, thì hai đoạn thẳng bằng nhau.

Bước 3: Kết luận

Cuối cùng, nếu cả hai điều kiện đã được chứng minh, ta có thể kết luận rằng B là trung điểm của đoạn thẳng AC theo định nghĩa đã nêu ở phần giới thiệu.

Một số ví dụ minh họa

Để làm rõ hơn về cách chứng minh trung điểm, chúng ta hãy xem xét một số ví dụ cụ thể.

Ví dụ 1

Giả sử ta có ba điểm A, B, C trong mặt phẳng với tọa độ cụ thể như sau:

• A(1, 2)
• B(3, 4)
• C(5, 6)

Ta cần chứng minh rằng B là trung điểm của đoạn thẳng AC. Bước 1: Xác định vị trí

• Kiểm tra xem B có nằm giữa A và C không. Ta thấy rằng trong tọa độ, B(3, 4) nằm giữa A(1, 2) và C(5, 6).

Bước 2: Tính độ dài AB và BC

• Độ dài AB = √((3 - 1)² + (4 - 2)²) = √(4 + 4) = √8
• Độ dài BC = √((5 - 3)² + (6 - 4)²) = √(4 + 4) = √8

Kết luận: Vì AB = BC, B là trung điểm của đoạn thẳng AC.

Ví dụ 2

Giả sử ta có ba điểm A(0, 0), B(2, 2), và C(4, 4). Chúng ta sẽ xem xét B có phải là trung điểm của AC hay không. Bước 1: Xác định vị trí

• Kiểm tra xem B có nằm giữa A và C không. Ta thấy rằng B(2, 2) nằm giữa A(0, 0) và C(4, 4).

Bước 2: Tính độ dài AB và BC

• Độ dài AB = √((2 - 0)² + (2 - 0)²) = √(4 + 4) = √8
• Độ dài BC = √((4 - 2)² + (4 - 2)²) = √(4 + 4) = √8

Kết luận: Vì AB = BC, B là trung điểm của đoạn thẳng AC.

Kết luận

Việc chứng minh một điểm là trung điểm của một đoạn thẳng không chỉ là một kỹ năng cơ bản trong hình học mà còn là nền tảng cho nhiều kiến thức toán học khác. Qua các bước chứng minh và ví dụ minh họa, chúng ta thấy rằng việc xác định và chứng minh trung điểm không hề khó khăn nếu ta nắm vững các khái niệm cơ bản và áp dụng đúng phương pháp.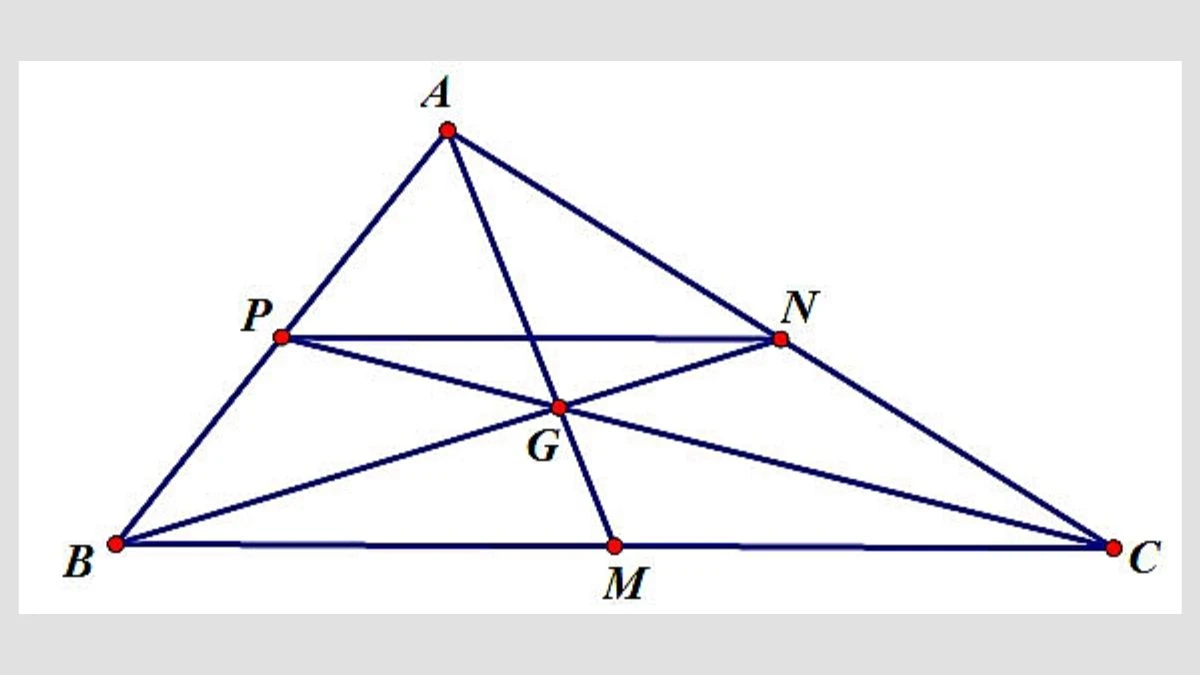 Hy vọng rằng bài viết này đã cung cấp cho bạn cái nhìn rõ ràng về cách chứng minh trung điểm, giúp bạn tự tin hơn trong các bài toán hình học. Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại chia sẻ để cùng nhau thảo luận!