Hệ số là gì và vai trò trong toán học

Khái niệm và vai trò trong toán học

Trong lĩnh vực toán học, có rất nhiều khái niệm và thuật ngữ mà chúng ta cần phải nắm rõ để có thể hiểu và áp dụng chúng trong các bài toán. Một trong những khái niệm quan trọng và thường gặp chính là khái niệm về một số nhân trong các biểu thức toán học. Đó chính là những gì mà chúng ta sẽ tìm hiểu trong bài viết này. Các hệ số này không chỉ có vai trò quan trọng trong toán học mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như vật lý, kinh tế và kỹ thuật. Để hiểu rõ hơn, trước tiên chúng ta cần phân tích cấu trúc của một biểu thức toán học. Trong một đa thức, ví dụ như x² - 5xy + 3 + y², sẽ có những thành phần gọi là số hạng. Mỗi số hạng này đều có một hệ số đi kèm, mà có thể là một số thực hoặc biến số. Hệ số chính là giá trị số mà mỗi số hạng được nhân với biến số trong biểu thức.

Các loại hệ số trong toán học

Hệ số tự do

Trong một đa thức, hệ số tự do là hệ số của hạng tử bậc 0, tức là hạng tử không chứa biến. Ví dụ, trong đa thức x² - 5xy + 3 + y², hạng tử 3 chính là hệ số tự do. Hệ số tự do có ý nghĩa quan trọng trong việc xác định giá trị của đa thức khi các biến số bằng 0.

Hệ số cao nhất

Hệ số cao nhất là hệ số của hạng tử có bậc cao nhất trong đa thức. Ví dụ, trong đa thức x³ - 3x² + 4x - 2, hệ số cao nhất là 1, vì 1 là hệ số của hạng tử x³. Hệ số cao nhất thường được sử dụng để xác định dạng của đồ thị của hàm số tương ứng với đa thức đó.

Hệ số góc

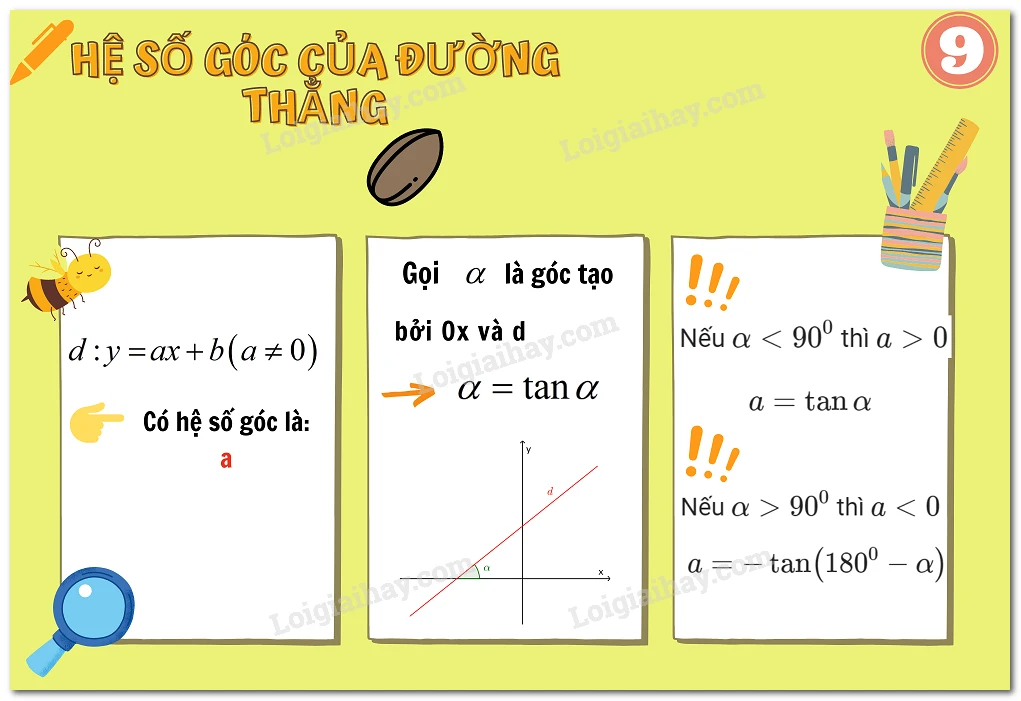
Hệ số góc là một khái niệm quan trọng trong hình học và đại số. Đối với một phương trình đường thẳng dạng y = ax + b, hệ số a chính là hệ số góc. Hệ số góc xác định độ dốc của đường thẳng, và có thể giúp chúng ta hiểu rõ hơn về xu hướng của các mối quan hệ giữa các biến.

Hệ số tỷ lệ

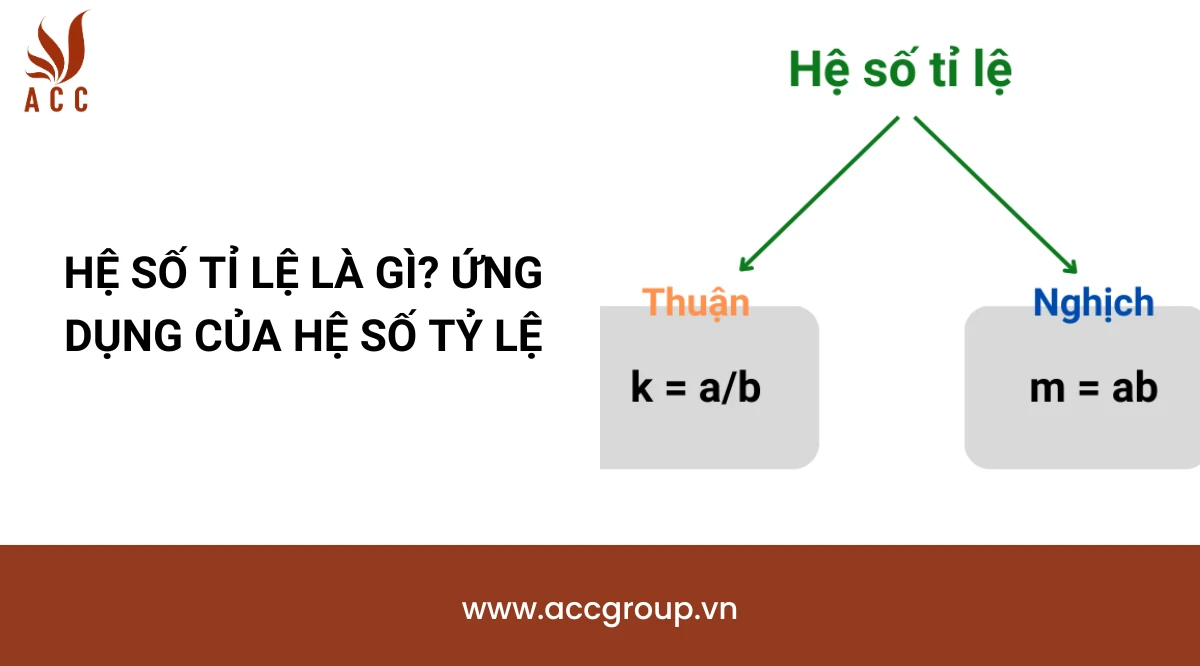
Trong thống kê và kinh tế, hệ số tỷ lệ được sử dụng để đo lường sự tương quan giữa hai yếu tố. Ví dụ, hệ số tỷ lệ giữa chi phí và doanh thu có thể cho biết mức độ hiệu quả trong việc sử dụng nguồn lực. Hệ số này thường được biểu diễn dưới dạng tỷ lệ phần trăm và có thể được tính toán dựa trên các số liệu thực tế.

Ứng dụng trong thực tế

Trong toán học

Có thể nói rằng, khái niệm về hệ số là rất đa dạng và phong phú, đặc biệt là trong toán học. Chúng tạo thành nền tảng cho việc giải quyết các bài toán phức tạp. Các hệ số không chỉ đơn thuần là các con số mà chúng còn mang lại những thông tin sâu sắc về cấu trúc của bài toán.

Trong vật lý

Trong vật lý, các hệ số cũng đóng một vai trò quan trọng. Ví dụ, trong các phương trình đại số mô tả các hiện tượng vật lý như chuyển động, lực, và năng lượng, hệ số mối quan hệ thường được sử dụng để thiết lập mối liên hệ giữa các đại lượng khác nhau. Hệ số ma sát, hệ số đàn hồi, và nhiều hệ số khác là minh chứng rõ ràng cho sự cần thiết của các hệ số trong việc mô tả và dự đoán các hiện tượng vật lý.

Trong kinh tế

Trong lĩnh vực kinh tế, hệ số cũng được sử dụng để đo lường sự hiệu quả và mối quan hệ giữa các biến số. Ví dụ, hệ số K trong kế toán thường được sử dụng để kiểm soát rủi ro về hóa đơn. Hệ số này giúp các nhà quản lý hiểu được mối quan hệ giữa chi phí và lợi nhuận, từ đó đưa ra các quyết định tài chính hợp lý.

Trong thống kê

Trong thống kê, các hệ số như hệ số tương quan, hệ số hồi quy đều có vai trò quan trọng trong việc phân tích và dự đoán dữ liệu. Hệ số tương quan giúp xác định mức độ mạnh yếu của mối quan hệ giữa hai biến. Hệ số hồi quy thì cho phép chúng ta dự đoán giá trị của một biến dựa trên giá trị của biến khác.

Kết luận

Khái niệm về hệ số trong toán học và các lĩnh vực khác không thể xem nhẹ. Chúng không chỉ đơn giản là các con số mà còn mang lại những thông tin sâu sắc về sự tương quan và mối quan hệ giữa các yếu tố. Từ hệ số tự do đến hệ số góc, mỗi loại hệ số đều có những ứng dụng và vai trò riêng trong việc giải quyết các bài toán khác nhau. Việc hiểu rõ các hệ số và ứng dụng của chúng sẽ giúp bạn có cái nhìn tổng quát hơn về không chỉ toán học mà còn các lĩnh vực khác như vật lý, kinh tế và thống kê. Chúng ta có thể khẳng định rằng, hệ số là một phần không thể thiếu trong tư duy toán học, giúp chúng ta hiểu rõ hơn về thế giới xung quanh. Thông qua bài viết này, hy vọng bạn sẽ có được những kiến thức bổ ích về khái niệm và ứng dụng của các hệ số, từ đó có thể áp dụng chúng vào trong học tập cũng như thực tế. Hãy cùng nhau khám phá và nghiên cứu sâu hơn về các hệ số để phát triển tư duy toán học của mình nhé!