Quỹ tích là gì và ý nghĩa trong hình học

Khái niệm về quỹ tích

Trong lĩnh vực hình học, có một khái niệm rất quan trọng và thú vị liên quan đến việc xác định vị trí của các điểm trong không gian. Đó chính là một tập hợp các điểm mà trong đó mỗi điểm đều thỏa mãn một hoặc nhiều điều kiện nhất định. Khái niệm này không chỉ đơn thuần là sự mô tả một hình dạng, mà còn thể hiện sự liên kết giữa vị trí của các điểm trong không gian.

Định nghĩa và ý nghĩa

Quỹ tích có thể được hiểu đơn giản là hình ảnh của tất cả các điểm mà một đối tượng có thể di chuyển tới, dựa vào những điều kiện cụ thể. Ví dụ, nếu chúng ta xem xét điểm A di chuyển trên một đường thẳng, thì quỹ tích của điểm A sẽ là chính đường thẳng đó. Nếu điểm A di chuyển với một khoảng cách nhất định từ một điểm cố định B, thì quỹ tích của A sẽ tạo thành một hình tròn với B là tâm. Không chỉ giới hạn trong những hình dạng đơn giản, quỹ tích còn có thể là những hình phức tạp hơn, như elip, parabol, hoặc hyperbol. Việc hiểu rõ về quỹ tích không chỉ giúp học sinh nắm vững kiến thức hình học, mà còn là nền tảng cho nhiều ứng dụng khoa học khác, như vật lý, kỹ thuật và khoa học máy tính.

Các loại quỹ tích cơ bản

Có nhiều loại quỹ tích khác nhau, mỗi loại đều có đặc điểm riêng và được sử dụng trong các tình huống khác nhau. Dưới đây là một số loại quỹ tích cơ bản thường gặp:

1. Quỹ tích của một điểm

Như đã đề cập ở phần trước, quỹ tích của một điểm có thể là một đường thẳng, một đường tròn hoặc những hình dạng khác tùy thuộc vào điều kiện di chuyển. Ví dụ, nếu một điểm di chuyển với khoảng cách không đổi x từ một điểm cố định, thì quỹ tích của điểm đó sẽ là một đường tròn.

2. Quỹ tích của một đoạn thẳng

Quỹ tích của một đoạn thẳng là các điểm nằm trên đường thẳng đó. Đây là một trong những hình dạng cơ bản nhất trong toán học. Khi chúng ta nói về quỹ tích của một đoạn thẳng, chúng ta thường đề cập đến sự thay đổi của một điểm trên đoạn thẳng đó.

3. Quỹ tích của một hình tròn

Hình tròn là một trong các hình dạng phổ biến nhất trong hình học. Quỹ tích của một điểm nằm trên hình tròn sẽ tạo thành chính hình tròn đó. Hình tròn có thể được mô tả bằng một phương trình đơn giản trong hệ tọa độ, giúp dễ dàng xác định vị trí của các điểm nằm trên nó.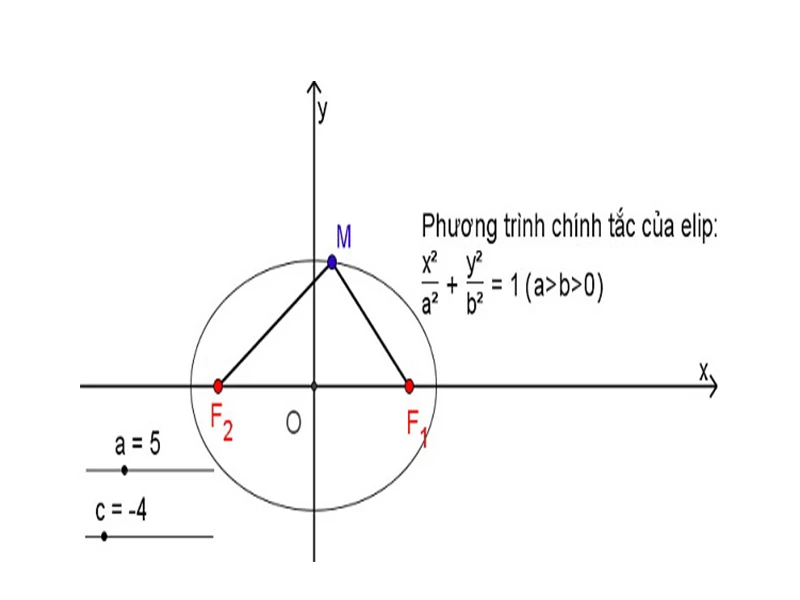

4. Quỹ tích của một hình elip

Quỹ tích của một điểm di chuyển quanh hai điểm cố định (gọi là tiêu điểm) với tổng khoảng cách từ hai tiêu điểm không đổi sẽ tạo thành một hình elip. Hình elip thường được sử dụng trong nhiều lĩnh vực như vật lý và thiên văn học.

Cách xác định quỹ tích

Việc xác định quỹ tích của một điểm hay một đoạn thẳng có thể thực hiện thông qua nhiều phương pháp khác nhau, tùy thuộc vào điều kiện và hình dạng cần tìm. Dưới đây là một số phương pháp phổ biến:

1. Sử dụng công thức toán học

Một trong những cách đơn giản nhất để tìm quỹ tích là sử dụng các công thức toán học. Ví dụ, để xác định quỹ tích của một điểm di chuyển với khoảng cách không đổi x từ một điểm cố định B, ta có thể sử dụng công thức của đường tròn: \[ (x - x_0)^2 + (y - y_0)^2 = r^2 \] Trong đó \((x_0, y_0)\) là tọa độ của điểm B, và r là khoảng cách từ B tới điểm A.

2. Sử dụng hình vẽ

Phương pháp này thường được sử dụng để xác định quỹ tích trong các bài tập học sinh. Học sinh có thể vẽ hình để trực quan hóa tình huống, từ đó dễ dàng hơn trong việc xác định quỹ tích.

3. Ứng dụng vào bài toán thực tế

Trong nhiều bài toán thực tế, việc xác định quỹ tích có thể giúp giải quyết các vấn đề liên quan đến chuyển động, quỹ đạo, hoặc các hiện tượng tự nhiên khác. Ví dụ, trong vật lý, quỹ tích của một chiếc xe di chuyển trên đường có thể được tính toán để dự đoán vị trí của nó trong tương lai.

Ứng dụng của quỹ tích trong cuộc sống

Khái niệm quỹ tích không chỉ giới hạn trong phạm vi toán học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Dưới đây là một số ứng dụng tiêu biểu:

1. Trong khoa học và kỹ thuật

Quỹ tích được sử dụng trong nhiều lĩnh vực khoa học và kỹ thuật, từ việc thiết kế hệ thống GPS đến các mô hình quỹ đạo của vệ tinh. Việc hiểu rõ về quỹ tích giúp các nhà khoa học và kỹ sư có thể dự đoán và điều chỉnh vị trí của các đối tượng trong không gian.

2. Trong đồ họa máy tính

Trong đồ họa máy tính, quỹ tích còn được sử dụng để tạo ra chuyển động mượt mà cho các đối tượng. Các thuật toán về quỹ tích thường được áp dụng để mô phỏng chuyển động của các vật thể trong không gian 3D.

3. Trong nghệ thuật và thiết kế

Nghệ sĩ và nhà thiết kế thường sử dụng khái niệm quỹ tích để tạo ra các tác phẩm nghệ thuật độc đáo. Họ có thể mô phỏng các hình dạng và đường nét bằng cách xác định quỹ tích của các điểm di chuyển.

4. Trong thiên văn học

Trong thiên văn học, quỹ tích là rất quan trọng để mô tả quỹ đạo của các hành tinh và ngôi sao. Các nhà thiên văn học sử dụng quỹ tích để xác định vị trí và chuyển động của các thiên thể trong không gian.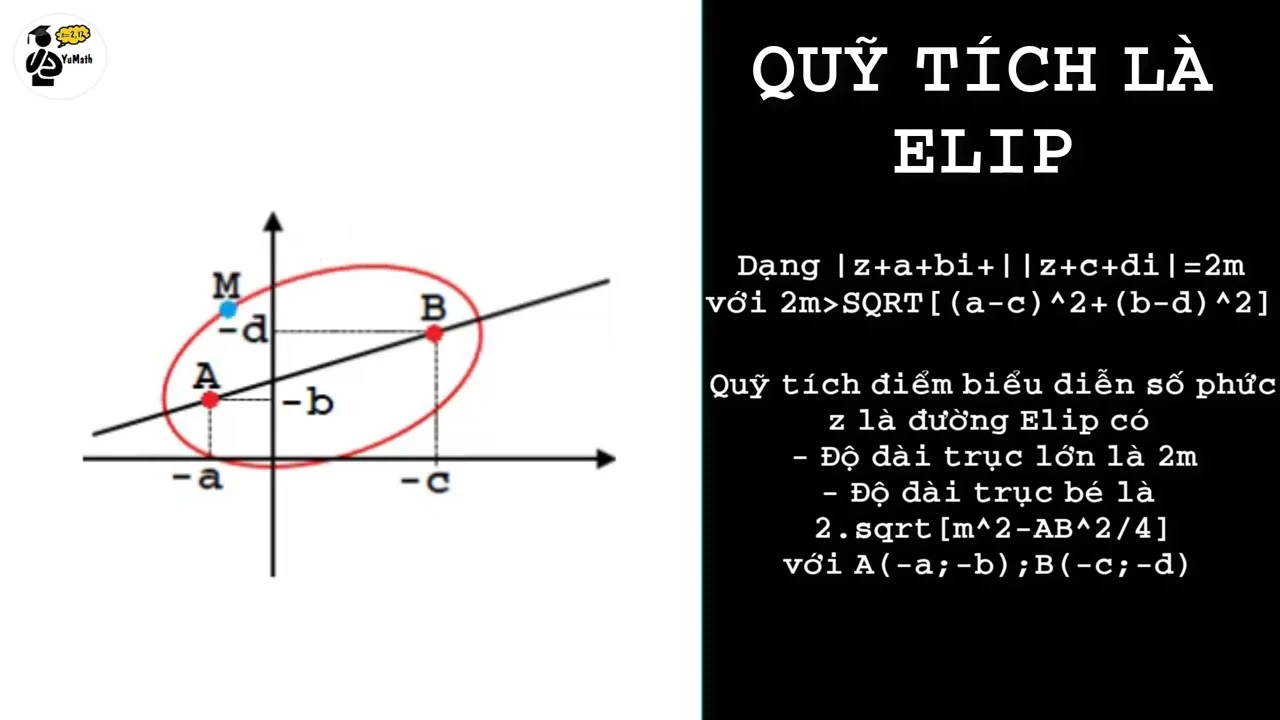

Kết luận

Khái niệm về quỹ tích là một phần quan trọng trong hình học và có nhiều ứng dụng thực tiễn trong đời sống và các lĩnh vực khoa học khác. Hiểu rõ quỹ tích giúp chúng ta không chỉ nắm vững kiến thức toán học mà còn áp dụng nó vào thực tiễn để giải quyết các vấn đề phức tạp. Việc nghiên cứu và khám phá thêm về quỹ tích sẽ mở ra nhiều cơ hội học hỏi và sáng tạo cho những ai đam mê với toán học và khoa học.