Cách chứng minh thẳng hàng ba điểm trong hình học

Giới thiệu về tính thẳng hàng trong hình học

Trong hình học, một khái niệm quan trọng mà chúng ta thường gặp là tính thẳng hàng của ba điểm. Ba điểm được gọi là thẳng hàng nếu chúng nằm trên cùng một đường thẳng. Việc chứng minh ba điểm thẳng hàng không chỉ là một phần thi trong các bài kiểm tra mà còn là một kỹ năng cơ bản trong toán học, giúp chúng ta hiểu rõ hơn về cấu trúc không gian và mối quan hệ giữa các điểm. Trong bài viết này, chúng ta sẽ đi sâu vào các phương pháp chứng minh ba điểm thẳng hàng, từ các cách đơn giản đến những phương pháp phức tạp hơn.

Các phương pháp chứng minh ba điểm thẳng hàng

Có nhiều cách để chứng minh rằng ba điểm nằm trên một đường thẳng. Dưới đây là một số phương pháp phổ biến mà bạn có thể áp dụng.

Sử dụng tính chất của góc bẹt

Một trong những phương pháp đơn giản nhất để chứng minh ba điểm thẳng hàng là sử dụng tính chất của góc bẹt. Nếu ba điểm A, B, C được sắp xếp sao cho góc AOB và góc BOC là hai góc kề bù, điều này có nghĩa là tổng của chúng bằng 180 độ. Khi đó, chúng ta có thể khẳng định rằng ba điểm A, B, C là thẳng hàng.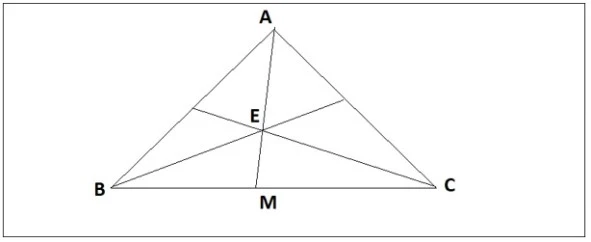

Sử dụng vectơ

Phương pháp này liên quan đến việc sử dụng toán học vectơ. Nếu ba điểm A, B, C có tọa độ trong không gian, chúng ta có thể chứng minh rằng chúng thẳng hàng bằng cách tính toán vectơ AB và vectơ AC. Nếu hai vectơ này đồng phương, điều đó có nghĩa là ba điểm A, B, C nằm trên cùng một đường thẳng. Cụ thể, nếu tồn tại một số k sao cho vectơ AB = k * vectơ AC, thì ba điểm này thẳng hàng.

Sử dụng các tính chất của tam giác

Một phương pháp khác để chứng minh ba điểm thẳng hàng là sử dụng các tính chất của tam giác. Cụ thể, nếu ba điểm A, B, C nằm trên cùng một đường thẳng, thì trung điểm của đoạn thẳng AB cũng sẽ nằm trên đường thẳng đó. Nếu chúng ta có một tam giác và biết rằng một trong các điểm nằm trên cạnh của tam giác, chúng ta có thể dễ dàng chứng minh rằng ba điểm thẳng hàng.

Sử dụng các định lý hình học

Một số định lý hình học có thể giúp chúng ta chứng minh ba điểm thẳng hàng. Ví dụ, định lý về hai tia đối nhau có thể được áp dụng để chứng minh tính thẳng hàng. Nếu chúng ta có hai tia đối nhau và biết rằng ba điểm nằm trên các tia này, chúng ta có thể kết luận rằng ba điểm đó thẳng hàng.

Một số ví dụ minh họa

Để hiểu rõ hơn về các phương pháp chứng minh, chúng ta hãy xem xét một số ví dụ cụ thể.

Ví dụ 1: Sử dụng góc bẹt

Giả sử chúng ta có ba điểm A, B, C. Nếu góc AOB và góc BOC là hai góc kề bù, chúng ta sẽ có:

• Góc AOB + Góc BOC = 180 độ

Từ đó, chúng ta có thể khẳng định rằng A, B, C là thẳng hàng.

Ví dụ 2: Sử dụng vectơ

Giả sử tọa độ của ba điểm A(1, 2), B(3, 4), C(5, 6). Chúng ta có thể tính vectơ AB và vectơ AC:

• Vectơ AB = B - A = (3-1, 4-2) = (2, 2)
• Vectơ AC = C - A = (5-1, 6-2) = (4, 4)

Nếu tồn tại một hằng số k sao cho (2, 2) = k*(4, 4), tức là k = 0.5, thì ba điểm A, B, C thẳng hàng.

Ví dụ 3: Sử dụng tính chất của tam giác

Giả sử chúng ta có tam giác ABC với điểm D là trung điểm của đoạn AB. Để chứng minh rằng ba điểm A, D, C thẳng hàng, chúng ta chỉ cần chỉ ra rằng D cũng nằm trên cùng một đường thẳng với A và C.

Tóm tắt

Việc chứng minh ba điểm thẳng hàng là một khái niệm cơ bản trong hình học mà bất kỳ học sinh nào cũng cần phải nắm rõ. Qua các phương pháp như sử dụng tính chất của góc bẹt, vectơ, tính chất của tam giác và các định lý hình học, chúng ta có thể dễ dàng chứng minh rằng ba điểm A, B, C là thẳng hàng. Các phương pháp này không chỉ giúp ích cho việc học tập mà còn tạo nền tảng vững chắc cho những kiến thức cao hơn trong hình học và toán học nói chung. Hãy nhớ rằng việc thành thạo các kỹ năng chứng minh sẽ giúp bạn tự tin hơn trong các kỳ thi và trong việc giải quyết các bài toán thực tế.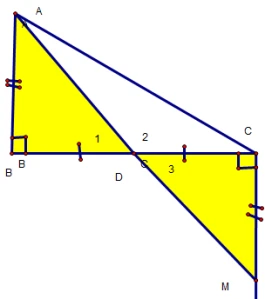 Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách chứng minh tính thẳng hàng của ba điểm. Nếu bạn có bất kỳ câu hỏi nào, hãy để lại ý kiến của bạn và chúng tôi sẽ cố gắng giải đáp.