Cách chứng minh ba điểm thẳng hàng dễ hiểu và hiệu quả

Khái niệm cơ bản về ba điểm thẳng hàng

Trong hình học, khái niệm về ba điểm thẳng hàng rất quan trọng. Ba điểm được coi là thẳng hàng nếu chúng nằm trên cùng một đường thẳng. Điều này có nghĩa là nếu bạn có ba điểm A, B, và C, thì chúng sẽ thẳng hàng nếu có thể nối chúng lại với nhau bằng một đường thẳng mà không cần phải rời tay. Trong thực tế, việc xác định ba điểm có thẳng hàng hay không có thể được thực hiện thông qua nhiều phương pháp khác nhau, bao gồm việc sử dụng góc bẹt, tiên đề Euclid, hoặc các tính chất hình học khác.

Các phương pháp chứng minh điểm thẳng hàng

1. Sử dụng tính chất góc bẹt

Một trong những phương pháp phổ biến nhất để chứng minh ba điểm thẳng hàng là sử dụng tính chất của góc bẹt. Theo định nghĩa, góc bẹt là góc có giá trị bằng 180 độ. Khi hai góc kề bù tạo thành một góc bẹt, điều này cho thấy rằng ba điểm liên quan đang nằm trên cùng một đường thẳng.

Ví dụ minh họa

Giả sử bạn có ba điểm A, B và C. Nếu bạn biết rằng góc ABC và góc ACB là hai góc kề bù và tổng của chúng bằng 180 độ, bạn có thể kết luận rằng A, B và C thẳng hàng.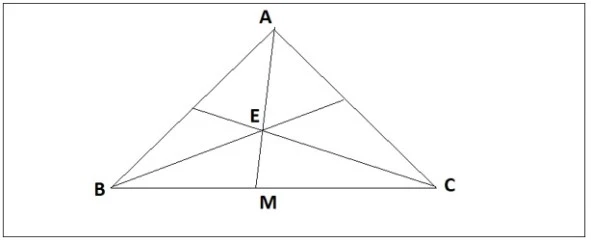

2. Sử dụng tiên đề Euclid

Euclid đã đặt ra nhiều tiên đề trong hình học, và một trong số đó liên quan đến việc ba điểm có thể nằm trên một đường thẳng. Tiên đề này khẳng định rằng: "Hai điểm có thể xác định một đường thẳng duy nhất". Dựa trên tiên đề này, nếu bạn có ba điểm A, B và C, và nếu bạn có thể xác định đường thẳng giữa A và B, sau đó giữa A và C, thì bạn có thể kết luận rằng A, B và C đang thẳng hàng.

Phương pháp chứng minh

• Bước 1: Vẽ đường thẳng AB.
• Bước 2: Vẽ đường thẳng AC.
• Bước 3: Nếu AB và AC trùng nhau tại một điểm, thì A, B và C thẳng hàng.

3. Sử dụng tính chất trung điểm

Một phương pháp khác để chứng minh ba điểm thẳng hàng là thông qua tính chất trung điểm. Nếu bạn có một đoạn thẳng, bạn có thể xác định trung điểm của đoạn thẳng đó. Giả sử bạn có các điểm A và B, và C là trung điểm của đoạn thẳng AB. Khi đó, A, B và C sẽ thẳng hàng. Điều này có thể được áp dụng trong nhiều tình huống khác nhau.

Các bài tập áp dụng

Bài tập 1

Cho ba điểm A, B và C với tọa độ A(1, 2), B(3, 6) và C(5, 10). Chứng minh rằng ba điểm này thẳng hàng. Giải:

• Tính độ dốc của đoạn thẳng AB:

- Độ dốc AB = (y2 - y1) / (x2 - x1) = (6 - 2) / (3 - 1) = 2.

• Tính độ dốc của đoạn thẳng BC:

- Độ dốc BC = (10 - 6) / (5 - 3) = 2.

• Vì độ dốc của AB và BC bằng nhau, nên A, B và C thẳng hàng.

Bài tập 2

Cho ba điểm A(0, 0), B(2, 2) và C(4, 4). Chứng minh rằng ba điểm này thẳng hàng bằng phương pháp góc bẹt. Giải:

• Vẽ hình với ba điểm A, B, C.
• Xác định các góc ∠ABC và ∠ACB.
• Nếu tổng của hai góc này bằng 180 độ, thì A, B và C thẳng hàng.

Kết luận

Chứng minh ba điểm thẳng hàng là một phần quan trọng trong hình học, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các điểm và các đường thẳng. Bằng cách áp dụng các phương pháp như tính chất góc bẹt, tiên đề Euclid, hoặc tính chất trung điểm, bạn có thể dễ dàng xác định xem ba điểm có thẳng hàng hay không. Với những kiến thức đã được trình bày, hy vọng bạn sẽ tự tin hơn trong việc giải quyết các bài toán liên quan đến ba điểm thẳng hàng.