
02/03/2025 10:45
Khái niệm cơ bản về các loại số
Trong toán học, hiểu biết về các loại số là điều cần thiết để phát triển tư duy logic và khả năng giải quyết vấn đề. Một trong những khái niệm cơ bản mà mỗi học sinh đều gặp phải là phân loại số thành hai nhóm chính: số nguyên và số thực. Trong số nguyên, có một phân loại đặc biệt được gọi là số chia hết cho hai. Để hiểu rõ hơn về khái niệm này, chúng ta sẽ đi sâu vào những đặc điểm, ứng dụng cũng như cách phân biệt giữa các loại số này.
Đặc điểm của số chia hết cho hai
Những số này có một đặc điểm nổi bật: khi chia cho hai, kết quả sẽ không có phần dư. Cụ thể, các số này bao gồm: 0, 2, 4, 6, 8, 10, 12, và tiếp tục theo quy luật của phép cộng 2. Một cách đơn giản để nhận diện loại số này là nhìn vào chữ số cuối cùng của nó. Nếu chữ số đó thuộc tập hợp {0, 2, 4, 6, 8}, thì số đó được phân loại là số chia hết cho hai. Ngoài ra, số chia hết cho hai có thể được biểu diễn dưới dạng công thức: n = 2k, trong đó n là số cần kiểm tra và k là bất kỳ số nguyên nào. Ví dụ, khi k = 1, n sẽ là 2; khi k = 2, n sẽ là 4; và cứ như vậy, số này có thể kéo dài vô hạn.Phân loại các loại số
1. Số chia hết cho hai
Như đã đề cập, những số này được xác định bằng cách chia cho hai và không có phần dư. Ví dụ: 10 chia cho 2 bằng 5, và 20 chia cho 2 bằng 10, đều là số nguyên dương.2. Số không chia hết cho hai
Ngược lại, những số không thể chia cho hai mà không có phần dư sẽ được gọi là số không chia hết cho hai. Chúng bao gồm: 1, 3, 5, 7, 9, 11, 13, và cứ tiếp tục. Một cách đơn giản để nhận diện chúng là nhìn vào chữ số tận cùng: nếu chữ số cuối cùng thuộc tập hợp {1, 3, 5, 7, 9}, thì số đó không chia hết cho hai.
Ứng dụng của số chia hết cho hai trong đời sống
Những số này không chỉ có ý nghĩa trong toán học mà còn có ứng dụng rộng rãi trong đời sống hàng ngày. Một số ứng dụng tiêu biểu bao gồm:1. Trong lĩnh vực công nghệ thông tin
Số chia hết cho hai thường được sử dụng trong các thuật toán lập trình, vì nhiều thuật toán được thiết kế để xử lý số liệu theo cặp. Việc phân loại số theo tính chất chẵn lẻ giúp tối ưu hóa quá trình xử lý dữ liệu.2. Trong các trò chơi và quản lý
Nhiều trò chơi và hoạt động giải trí sử dụng số chia hết cho hai để quyết định lượt chơi hoặc phân chia đội. Ví dụ, khi chia đội trong một trò chơi thể thao, việc sử dụng số chẵn giúp đảm bảo số lượng người tham gia trong mỗi đội là đều.3. Trong thống kê và phân tích dữ liệu
Khi thực hiện các phân tích thống kê, việc phân loại số liệu thành hai nhóm chẵn và lẻ có thể giúp nhà phân tích rút ra các kết luận cụ thể hơn. Điều này giúp trong việc dự đoán xu hướng và mẫu số liệu.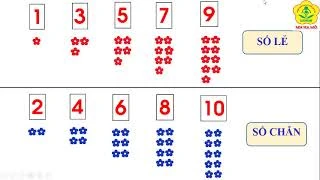
Cách nhận biết số chia hết cho hai một cách dễ dàng
Việc nhận biết số chia hết cho hai là rất đơn giản. Dưới đây là một số mẹo và kỹ thuật giúp bạn dễ dàng phân biệt:1. Kiểm tra chữ số cuối cùng
Đây là phương pháp nhanh chóng và hiệu quả nhất. Chỉ cần nhìn vào chữ số cuối cùng của số cần kiểm tra:- Nếu số đó kết thúc bằng 0, 2, 4, 6, hoặc 8, thì nó là số chia hết cho hai.
- Nếu số đó kết thúc bằng 1, 3, 5, 7, hoặc 9, thì nó không phải số chia hết cho hai.
2. Sử dụng công thức
Bạn có thể áp dụng công thức: n = 2k, với k là một số nguyên. Nếu bạn có thể tìm được một giá trị k sao cho n chia hết cho 2, thì số đó là số chia hết cho hai.
3. Thực hành qua bài tập
Một trong những cách hiệu quả nhất để ghi nhớ là thực hành qua các bài tập. Hãy làm các bài tập tương ứng với việc phân loại số chẵn và lẻ để củng cố kiến thức.Kết luận
Tóm lại, việc hiểu rõ về số chia hết cho hai không chỉ giúp trong việc học tập mà còn rất cần thiết trong các lĩnh vực khác nhau trong đời sống. Qua bài viết này, hy vọng bạn đã có cái nhìn sâu sắc hơn về khái niệm này, cách nhận diện và ứng dụng của nó trong thực tế. Hãy luôn nhớ rằng, việc nhận biết những điều tưởng chừng như đơn giản cũng có thể mang lại nhiều lợi ích lớn trong học tập cũng như trong cuộc sống hàng ngày.
Link nội dung: https://galileo.edu.vn/blog-a15721.html