Công thức tính toán cơ bản giúp nâng cao kỹ năng tài chính

I. Giới thiệu về các phương pháp tính toán

Trong cuộc sống hàng ngày, chúng ta thường xuyên phải đối mặt với các phép toán tính toán. Từ việc mua sắm, tính lãi suất ngân hàng cho đến xác định tỉ lệ phần trăm trong báo cáo tài chính, việc nắm vững các phương pháp tính toán cơ bản là rất quan trọng. Không chỉ giúp bạn tiết kiệm thời gian mà còn nâng cao khả năng phân tích và đánh giá thông tin một cách chính xác. Trong bài viết này, chúng ta sẽ tìm hiểu về các phương pháp tính toán cơ bản, từ cách tính phần trăm cho đến công suất, thể tích và nhiều hơn nữa. Những kiến thức này sẽ giúp bạn tự tin hơn trong việc giải quyết các bài toán thực tiễn.

II. Phần trăm - Một khái niệm quan trọng trong toán học

1. Định nghĩa phần trăm

Phần trăm là một cách diễn đạt số lượng dưới dạng tỷ lệ với 100. Ví dụ, 50% có nghĩa là 50 trên 100. Tính phần trăm giúp chúng ta dễ dàng so sánh và đánh giá các giá trị khác nhau. Đặc biệt, trong kinh doanh và tài chính, phần trăm thường được sử dụng để tính lãi suất, giảm giá và các thông số quan trọng khác.

2. Công thức tính phần trăm

Để tính phần trăm, bạn có thể sử dụng công thức sau: \[ \text{Phần trăm} = \left( \frac{\text{Số cần tính}}{\text{Tổng}} \right) \times 100 \] Trong đó:

• Số cần tính là giá trị bạn muốn tìm phần trăm.
• Tổng là giá trị tổng thể mà số đó thuộc về.

Ví dụ: Nếu bạn có 20 trái cây trong giỏ và muốn biết tỉ lệ của táo trong số đó, với 5 quả táo, bạn sẽ tính như sau: \[ \text{Phần trăm táo} = \left( \frac{5}{20} \right) \times 100 = 25\% \]

3. Các loại tính phần trăm phổ biến

• Phần trăm tăng trưởng: Để tính phần trăm tăng trưởng giữa hai giá trị, bạn sử dụng công thức:

\[ \text{Phần trăm tăng trưởng} = \left( \frac{\text{Giá trị mới} - \text{Giá trị cũ}}{\text{Giá trị cũ}} \right) \times 100 \]

• Phần trăm giảm: Tương tự, khi tính phần trăm giảm, bạn có thể sử dụng:

\[ \text{Phần trăm giảm} = \left( \frac{\text{Giá trị cũ} - \text{Giá trị mới}}{\text{Giá trị cũ}} \right) \times 100 \]

III. Tính công suất - Một khía cạnh không thể thiếu

1. Định nghĩa công suất

Công suất là một khái niệm trong vật lý và kỹ thuật, thể hiện khả năng thực hiện công việc trong một khoảng thời gian nhất định. Nó thường được đo bằng watt (W) trong hệ đơn vị SI. Công suất có thể được áp dụng trong nhiều lĩnh vực như điện năng, cơ khí và hóa học.

2. Công thức tính công suất

Công thức tính công suất cơ bản là: \[ P = \frac{W}{t} \] Trong đó:

• \( P \) là công suất (đơn vị là watt),
• \( W \) là công (đơn vị là joule),
• \( t \) là thời gian (đơn vị là giây).

Ví dụ, nếu bạn thực hiện một công việc mà mất 10 joule năng lượng trong 2 giây, công suất sẽ được tính như sau: \[ P = \frac{10}{2} = 5 \text{ W} \]

3. Các ứng dụng của công suất

Công suất được sử dụng rộng rãi trong ngành điện, từ việc tính toán công suất tiêu thụ của các thiết bị điện gia dụng cho đến việc thiết kế hệ thống điện công nghiệp. Việc nắm vững các công thức và phương pháp tính công suất không chỉ giúp bạn tiết kiệm năng lượng mà còn giúp đảm bảo an toàn trong việc sử dụng thiết bị điện.

IV. Thể tích - Khám phá không gian ba chiều

1. Định nghĩa thể tích

Thể tích là khái niệm dùng để đo không gian mà một vật thể chiếm giữ. Thể tích được đo bằng đơn vị khối (m³, lít, gallon, v.v.). Việc biết cách tính thể tích rất quan trọng trong nhiều lĩnh vực, từ xây dựng đến hóa học.

2. Công thức tính thể tích

Mỗi loại hình học sẽ có công thức tính thể tích riêng. Dưới đây là một số công thức phổ biến:

• Hình lập phương:

\[ V = a^3 \] (với \( a \) là độ dài cạnh)

• Hình hộp chữ nhật:

\[ V = a \times b \times h \] (với \( a \), \( b \), \( h \) lần lượt là chiều dài, chiều rộng và chiều cao)

• Hình trụ:

\[ V = \pi r^2 h \] (với \( r \) là bán kính đáy và \( h \) là chiều cao)

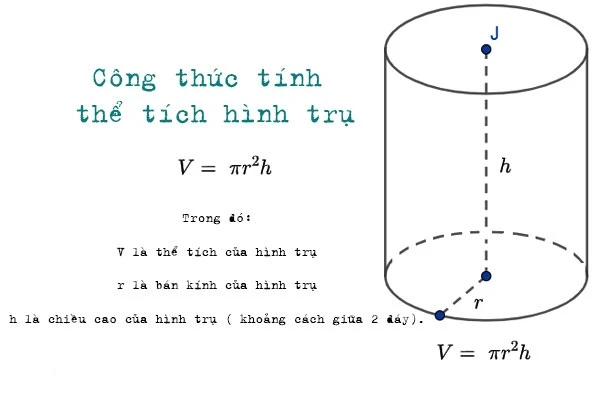
3. Ứng dụng của thể tích trong thực tế

Thể tích được áp dụng trong nhiều lĩnh vực như nông nghiệp, thực phẩm và y tế. Ví dụ, trong nông nghiệp, việc tính thể tích của nước cần cho cây trồng là rất quan trọng để đảm bảo cây phát triển tốt. Trong ngành thực phẩm, việc biết thể tích giúp xác định số lượng nguyên liệu cần thiết cho sản xuất.

V. Kết luận

Sử dụng các công thức và phương pháp tính toán là một kỹ năng thiết yếu trong cuộc sống hàng ngày. Từ việc tính phần trăm, công suất cho đến thể tích, những kiến thức này không chỉ giúp bạn nâng cao khả năng tính toán mà còn tăng cường khả năng phân tích và đưa ra quyết định chính xác. Hãy nắm vững các công thức và áp dụng chúng vào thực tiễn, bạn sẽ nhận thấy sự tiện lợi và hiệu quả mà chúng mang lại. Hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin bổ ích và cần thiết để bạn có thể tự tin hơn trong việc giải quyết các bài toán tính toán trong cuộc sống hàng ngày.