Coefficient là gì và vai trò của nó trong toán học

Giới Thiệu

Trong toán học và thống kê, việc sử dụng các hệ số là rất phổ biến. Chúng không chỉ xuất hiện trong các phương trình mà còn đóng vai trò quan trọng trong việc phân tích dữ liệu. Việc hiểu rõ về hệ số không chỉ giúp bạn trong môn toán mà còn giúp bạn áp dụng vào nhiều lĩnh vực khác nhau như kinh tế, khoa học xã hội, và nhiều ứng dụng thực tiễn khác. Hệ số có thể được hiểu là một giá trị số mà nó điều chỉnh, hoặc nhân với một ký hiệu, biến số nào đó. Chúng giúp chúng ta biểu diễn mối quan hệ giữa các biến và nhấn mạnh tầm quan trọng của các giá trị cụ thể trong các công thức.

Hệ Số Trong Toán Học

Trong toán học, hệ số thường xuất hiện trong các đa thức. Một đa thức là một biểu thức có chứa nhiều hạng tử mà mỗi hạng tử đều bao gồm một biến và một hệ số. Ví dụ, trong biểu thức toán học như \( 3x^2 + 2x + 5 \), số \( 3 \) là hệ số đứng trước biến \( x^2 \), số \( 2 \) là hệ số đứng trước biến \( x \), và \( 5 \) là một hạng tử không chứa biến. Ngoài ra, hệ số cũng thường được sử dụng trong các phương trình tuyến tính. Một phương trình dạng \( y = mx + b \) trong đó \( m \) là hệ số của biến \( x \), thể hiện độ dốc của đường thẳng trên đồ thị. Hệ số này rất quan trọng trong việc xác định hướng đi của đường thẳng.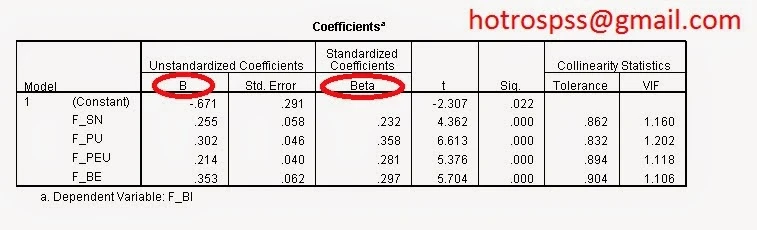

Các Loại Hệ Số

Có rất nhiều loại hệ số khác nhau, và mỗi loại được sử dụng cho các mục đích khác nhau. Dưới đây là một số loại hệ số phổ biến trong thống kê và nghiên cứu khoa học:

1. Hệ Số Tương Quan

Hệ số tương quan (Correlation Coefficient) dùng để đo lường mối quan hệ giữa hai biến số. Hệ số này nằm trong khoảng từ -1 đến 1. Nếu hệ số bằng 1, điều đó có nghĩa là có mối quan hệ tích cực hoàn hảo giữa hai biến. Ngược lại, nếu hệ số bằng -1, có nghĩa là có mối quan hệ tiêu cực hoàn hảo. Một hệ số bằng 0 cho thấy không có mối quan hệ nào giữa các biến. Ví dụ, nếu bạn đang nghiên cứu mối quan hệ giữa số giờ học và điểm thi, một hệ số tương quan cao sẽ cho thấy rằng các sinh viên học nhiều hơn thường có điểm cao hơn.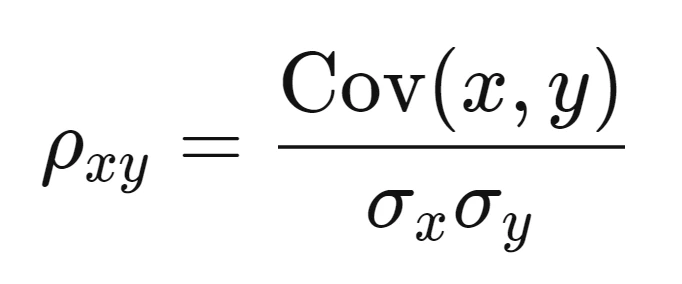

2. Hệ Số Biến Thiên

Hệ số biến thiên (Coefficient of Variation - CV) được sử dụng để đo độ biến động của một tập hợp dữ liệu. Nó được tính bằng tỉ lệ giữa độ lệch chuẩn và giá trị trung bình của tập dữ liệu. Hệ số này thường được sử dụng trong nghiên cứu kinh tế và tài chính để so sánh mức độ biến động giữa các loại tài sản khác nhau.

3. Hệ Số Xác Định

Hệ số xác định (Coefficient of Determination) là một thước đo trong phân tích hồi quy. Nó cho biết phần trăm biến thiên của biến phụ thuộc được giải thích bởi biến độc lập. Hệ số này cũng nằm trong khoảng từ 0 đến 1. Một giá trị gần 1 cho thấy mô hình hồi quy hoạt động tốt, trong khi giá trị gần 0 cho thấy mô hình không giải thích được nhiêu biến thiên.

4. Hệ Số Gini

Hệ số Gini được sử dụng để đo lường sự phân bổ thu nhập trong một dân số. Giá trị này dao động từ 0 đến 1, với 0 biểu thị sự bình đẳng hoàn hảo (tất cả mọi người có cùng một thu nhập) và 1 biểu thị sự bất bình đẳng tuyệt đối (một người nắm giữ toàn bộ thu nhập). Hệ số Gini thường được sử dụng trong nghiên cứu kinh tế để phân tích mức độ bất bình đẳng trong xã hội.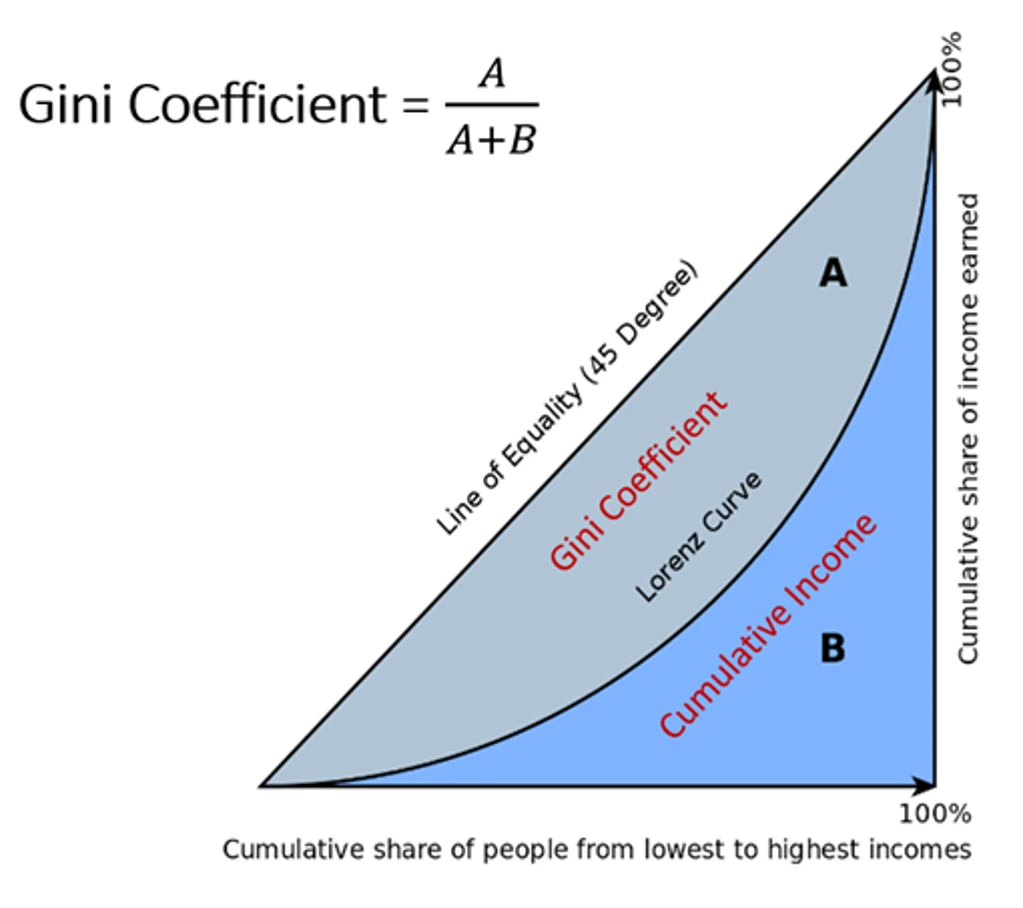

Ứng Dụng Của Hệ Số Trong Thực Tế

Hệ số không chỉ có ý nghĩa lý thuyết mà còn có nhiều ứng dụng trong thực tế. Dưới đây là một số ví dụ về ứng dụng của hệ số trong các lĩnh vực khác nhau:

1. Trong Kinh Tế

Hệ số thường được sử dụng để phân tích độ nhạy của các biến số trong kinh tế. Ví dụ, doanh nghiệp có thể sử dụng hệ số tương quan để xác định mối quan hệ giữa chi phí quảng cáo và doanh thu. Những thông tin này giúp họ đưa ra quyết định đúng đắn hơn về ngân sách cho quảng cáo.

2. Trong Khoa Học Xã Hội

Trong lĩnh vực khoa học xã hội, các nhà nghiên cứu sử dụng hệ số để phân tích dữ liệu khảo sát. Bằng cách tính toán hệ số tương quan, họ có thể xác định mối quan hệ giữa các yếu tố như trình độ học vấn và thu nhập. Điều này giúp các nhà hoạch định chính sách hiểu rõ hơn về xã hội mình đang sống.

3. Trong Y Tế

Trong ngành y tế, hệ số cũng đóng vai trò quan trọng trong việc đánh giá sự hiệu quả của các phương pháp điều trị. Hệ số xác định có thể được sử dụng để đo lường mức độ cải thiện sức khỏe của bệnh nhân sau khi điều trị.

Kết Luận

Hệ số là một thành phần không thể thiếu trong toán học và thống kê. Chúng không chỉ giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các biến số mà còn giúp chúng ta áp dụng các kiến thức này vào thực tế. Việc nắm bắt và áp dụng các loại hệ số một cách chính xác có thể mang lại lợi ích lớn trong nhiều lĩnh vực, từ kinh tế đến y tế và khoa học xã hội. Việc hiểu rõ về hệ số và các ứng dụng của nó sẽ giúp bạn tự tin hơn khi đối diện với các bài toán và phân tích dữ liệu trong cuộc sống hàng ngày. Chính vì vậy, hãy đầu tư thời gian để tìm hiểu và làm quen với các khái niệm này, vì chúng sẽ mang lại nhiều giá trị cho bạn trong tương lai.