
09/01/2025 04:15
Tính Diện Tích Xung Quanh Hình Hộp Chữ Nhật Đúng Cách
Hình hộp chữ nhật là một trong những hình không gian cơ bản trong toán học với đặc điểm cấu trúc đơn giản nhưng lại có nhiều ứng dụng trong thực tế. Việc tính diện tích xung quanh của hình hộp chữ nhật không những giúp bạn hiểu về hình học mà còn có thể ứng dụng trong các bài toán thực tiễn. Bài viết này sẽ đi sâu vào công thức tính diện tích xung quanh hình hộp chữ nhật cũng như hướng dẫn chi tiết cách áp dụng trong các tình huống cụ thể.
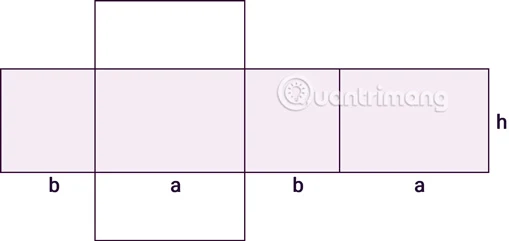


Hình Hộp Chữ Nhật Là Gì?

Khái Niệm
Hình hộp chữ nhật là một hình không gian có 6 mặt, tất cả các mặt đều là hình chữ nhật. Nó có tổng cộng 8 đỉnh và 12 cạnh. Trong đó, hai mặt đáy sẽ song song với nhau và được xác định bởi chiều dài và chiều rộng của hình hộp.Đặc Điểm Cấu Trúc
- Mặt đáy: Hai mặt đối diện song song với nhau.
- Mặt bên: Các mặt còn lại, thường được gọi là mặt bên của hình hộp.
Công Thức Tính Diện Tích Xung Quanh Hình Hộp Chữ Nhật
Cách Tính Diện Tích Xung Quanh
Diện tích xung quanh của hình hộp chữ nhật được tính bằng cách lấy chu vi đáy nhân với chiều cao. Công thức: \[ S_{xung\ quanh} = P \times h \] Trong đó:- \( P \) là chu vi đáy tính bằng \( P = 2 \times (a + b) \).
- \( h \) là chiều cao của hình hộp.
Ứng Dụng Công Thức
Để tính diện tích xung quanh, bạn cần biết chiều dài, chiều rộng và chiều cao của hình hộp. Dưới đây là mô hình để thực hiện phép tính:- Tính chu vi đáy: \( P = 2 \times (a + b) \)
- Nhân với chiều cao: \( S_{xung\ quanh} = P \times h \)
Công Thức Tính Diện Tích Toàn Phần Hình Hộp Chữ Nhật
Cách Tính Diện Tích Toàn Phần
Diện tích toàn phần hình hộp chữ nhật là tổng diện tích của tất cả 6 mặt của hình hộp. Công thức: \[ S_{toàn\ phần} = S_{xung\ quanh} + 2 \times S_{đáy} \] Trong đó:- \( S_{đáy} = a \times b \) là diện tích của một mặt đáy.
Thực Hiện Phép Tính
- Tính diện tích đáy: \( S_{đáy} = a \times b \)
- Thay vào công thức tính diện tích toàn phần:
Công Thức Tính Chiều Cao Hình Hộp Chữ Nhật
Từ công thức tính diện tích xung quanh, bạn có thể suy ra chiều cao.Cách Tính Chiều Cao
Công thức: \[ h = \frac{S_{xung\ quanh}}{P} \] Hãy nhớ rằng cần phải tính chu vi trước khi áp dụng công thức:- Tính chu vi: \( P = 2 \times (a + b) \)
- Tính chiều cao: Sử dụng công thức ở trên.
Ví Dụ Cụ Thể Về Tính Diện Tích Hình Hộp Chữ Nhật
Ví dụ 1: Tính Diện Tích Xung Quanh
Cho hình hộp chữ nhật có chiều dài \( a = 20 \)m, chiều rộng \( b = 7 \)m, chiều cao \( h = 10 \)m.- Tính chu vi đáy:
- Tính diện tích xung quanh:
Ví dụ 2: Tính Diện Tích Toàn Phần
Cho hình hộp với chiều dài \( 5.4 \)cm, chiều rộng \( 2 \)cm, chiều cao \( 3 \)cm.- Tính chu vi đáy:
- Tính diện tích xung quanh:
- Tính diện tích đáy:
- Tính diện tích toàn phần:
Kết Luận
Hình hộp chữ nhật không chỉ là một hình học cơ bản mà còn đóng vai trò quan trọng trong nhiều lĩnh vực như kiến trúc, xây dựng và thiết kế. Việc nắm vững cách tính diện tích xung quanh và toàn phần giúp bạn có thể áp dụng nhanh chóng vào các bài toán thực tiễn. Nếu bạn còn bất kỳ thắc mắc nào về tính diện tích xung quanh hình hộp chữ nhật, đừng ngần ngại để lại câu hỏi trong phần bình luận!
Link nội dung: https://galileo.edu.vn/tinh-dien-tich-xung-quanh-hinh-hop-chu-nhat-dung-cach-a14917.html