Tính Diện Tích Xung Quanh Hình Học Đơn Giản

Trong toán học, tính diện tích xung quanh là một trong những yếu tố quan trọng giúp chúng ta hiểu rõ hơn về kích thước và dung tích của các hình khối. Hình hộp chữ nhật là một trong những hình khối thường được sử dụng, và bài viết này sẽ cung cấp cho bạn những kiến thức cần thiết về cách tính diện tích xung quanh của nó cùng các dạng bài tập thường gặp.

1. Diện Tích Xung Quanh Của Hình Hộp Chữ Nhật

a. Định Nghĩa

Diện tích xung quanh của hình hộp chữ nhật được định nghĩa là tổng diện tích của bốn mặt bên của hình hộp đó. Điều này giúp chúng ta hình dung được kích thước bên ngoài mà không tính đến diện tích của các mặt đáy.

b. Công Thức Tính

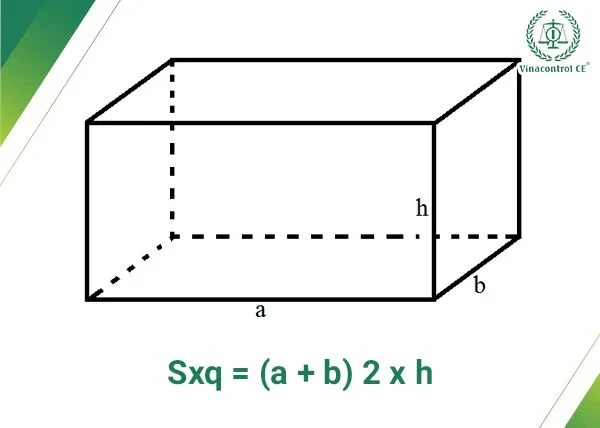
Để tính diện tích xung quanh của hình hộp chữ nhật, chúng ta sử dụng công thức sau: Sxq = (a + b) × 2 × h Trong đó:

• a: Chiều dài của hình hộp
• b: Chiều rộng của hình hộp
• h: Chiều cao của hình hộp

Chúng ta có thể hình dung công thức này thông qua hình ảnh: hệ số (a + b) là chu vi của mặt đáy, và nhân với chiều cao (h) để đưa ra diện tích.

Chứng Minh Công Thức

Hình hộp chữ nhật có chiều dài a, chiều rộng b, và chiều cao h. Diện tích xung quanh được tính như sau:

• Tổng diện tích của hai mặt bên: \(S_{mặt bên} = a \cdot h \times 2 + b \cdot h \times 2 = (a + b) \times 2 \cdot h\)

Hình minh họa bổ sung

Công thức tính diện tích xung quanh của hình hộp chữ nhật

2. Diện Tích Toàn Phần Của Hình Hộp Chữ Nhật

a. Định Nghĩa

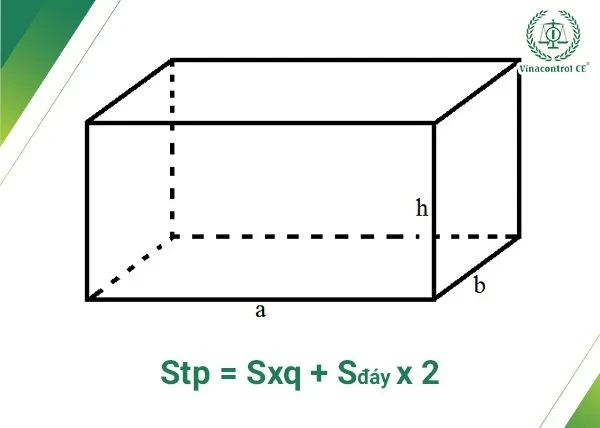
Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích của hai đáy của nó. Điều này có nghĩa là nó phản ánh toàn bộ diện tích bề mặt của hình hộp.

b. Công Thức Tính

Để tính diện tích toàn phần, ta sử dụng công thức sau: Stp = Sxq + Sđáy × 2 = (a + b) × 2 × h + 2 × a × b Trong đó:

• Sđáy: Diện tích của một đáy (a × b)

Hình minh họa bổ sung

Công thức tính diện tích toàn phần của hình hộp chữ nhật

3. Các Công Thức Khác Về Hình Hộp Chữ Nhật

a. Chu Vi Đáy Hình Hộp Chữ Nhật

Chu vi của đáy hình hộp chữ nhật là chu vi của hình chữ nhật ở đáy: Pđáy = 2 × (a + b)

b. Tổng Độ Dài Các Cạnh

Tổng độ dài của các cạnh của hình hộp chữ nhật có thể tính bằng công thức: P = 4 × (a + b + c) Trong đó:

• a, b, c lần lượt là chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật.

c. Diện Tích Mặt Bên

Diện tích mặt bên của hình hộp chữ nhật được tính bằng: Smb = 2 × (a × h + b × h)

d. Tính Chiều Cao Hình Hộp Chữ Nhật

Để tính chiều cao (h) của hình hộp chữ nhật, bạn cần biết diện tích mặt bên và kích thước chiều dài, chiều rộng của đáy: h = Smb / 2 × (a + b)

4. Lưu Ý Khi Làm Bài Tập Tính Diện Tích

Khi làm bài tập liên quan đến tính diện tích, có một số lưu ý quan trọng cần ghi nhớ:

• Đơn Vị Đo: Nếu độ dài các cạnh có đơn vị khác nhau, cần quy đổi về cùng một đơn vị đo độ dài.
• So Sánh Diện Tích: Nếu các diện tích cần so sánh có đơn vị đo khác nhau, hãy quy đổi về cùng một đơn vị đo trước khi tiến hành so sánh.
• Kiểm Tra Kết Quả: Bạn nên kiểm tra lại kết quả ít nhất 2 lần để đảm bảo tính chính xác.

5. Các Dạng Bài Tập Thường Gặp và Hướng Dẫn Giải

Dạng 1: Tính Diện Tích Xung Quanh Hoặc Diện Tích Toàn Phần

Phương pháp: Áp dụng công thức tính diện tích xung quanh hoặc diện tích toàn phần. Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 5cm, chiều rộng 7cm và chiều cao 3cm. Bài giải:

• Diện tích xung quanh của hình hộp chữ nhật đó là:

Sxq = (5 + 7) × 2 × 3 = 78 (cm²)

• Diện tích toàn phần của hình hộp chữ nhật đó là:

Stp = Sxq + (5 × 7) × 2 = 78 + 70 = 148 (cm²) Đáp số: Diện tích xung quanh: 78 cm² | Diện tích toàn phần: 148 cm²

Dạng 2: Biết Diện Tích Xung Quanh Hoặc Diện Tích Toàn Phần, Tìm Chu Vi Đáy Hoặc Chiều Cao

Phương pháp: Từ công thức Sxq = (a + b) × 2 × h:

• Tìm chiều cao: h = Sxq / [(a + b) × 2]
• Tìm tổng chu vi đáy: (a + b) × 2 = Sxq / h

Ví dụ: Cho hình hộp chữ nhật có diện tích xung quanh là 217,5 m² và nửa chu vi mặt đáy bằng 14,5 m. Tính chiều cao của hình hộp chữ nhật đó. Bài giải:

• Chu vi mặt đáy:

14,5 × 2 = 29 (m)

• Chiều cao:

217,5 / 29 = 7,5 (m) Đáp số: 7,5 m

Dạng 3: Toán Có Lời Văn (Tìm Diện Tích Hộp, Căn Phòng, Sơn Tường)

Phương pháp: Xác định diện tích cần tìm là diện tích xung quanh hay diện tích toàn phần trước tiên, sau đó áp dụng quy tắc tương ứng. Ví dụ: Một căn phòng hình hộp chữ nhật có được thông số chi tiết tương tự như trên. Bài giải: Áp dụng các công thức tương tự để tìm diện tích cần thiết.

6. Bài Tập Vận Dụng Tại Nhà

Dưới đây là một số bài tập bạn có thể thực hành tại nhà:

• Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có:

a) Chiều dài 25 cm, chiều rộng 15 cm và chiều cao 12 cm. b) Chiều dài 7,6 dm, chiều rộng 4,8 dm và chiều cao 2,5 dm. c) Chiều dài 4/5 m, chiều rộng 2/5 m và chiều cao 3/5 cm.

• Tính diện tích tôn dùng để làm hộp không nắp với kích thước cho trước.
• Dán giấy màu với kích thước quy định, tính diện tích giấy lớn hơn.
• Từ diện tích xung quanh và chiều cao, tìm chu vi đáy.
• Tính diện tích bìa dùng để làm hộp không bao gồm mép dán.
• Tính diện tích quét vôi trong phòng, nhớ đến diện tích của cửa.
• Bài toán có điều kiện về kích thước và diện tích xung quanh.
• Tính lượng sơn đã sử dụng cho thùng thùng không nắp với kích thước quy định.

Trên đây là toàn bộ nội dung về tính diện tích xung quanh và toàn phần của hình hộp chữ nhật. Hy vọng rằng bài viết đã cung cấp cho bạn nhiều kiến thức hữu ích và giúp bạn thực hành tốt hơn trong việc tính toán này.

Tham khảo

• Bảng quy đổi đơn vị tổng hợp trực tuyến
• Công thức tính diện tích hình chữ nhật
• Công thức tính diện tích hình lập phương

--- Hy vọng với những thông tin trên, bạn sẽ cảm thấy tự tin hơn để tìm hiểu và áp dụng trong các bài học và bài tập của mình!