Cách tính diện tích tam giác khi biết 3 cạnh

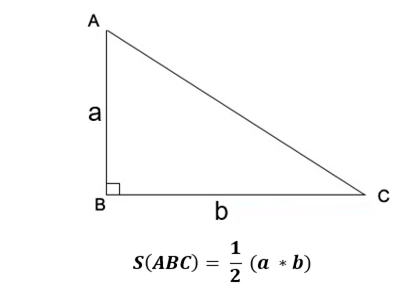
Tính Diện Tích Tam Giác Khi Biết 3 Cạnh: Hướng Dẫn Chi Tiết và Công Thức

Tính diện tích tam giác là một trong những bài toán cơ bản trong toán học, đặc biệt là khi bạn có thông tin về ba cạnh của tam giác. Trong bài viết này, The Dewey Schools sẽ hướng dẫn bạn chi tiết cách tính diện tích tam giác khi biết ba cạnh, thông qua công thức Heron. Chúng ta sẽ cùng nhau khám phá tài liệu này để làm chủ được phương pháp này nhé!

Định Nghĩa và Tính Chất Của Hình Tam Giác

Định Nghĩa Hình Tam Giác

Tam giác là một hình đa giác có ba cạnh và ba đỉnh. Các cạnh của tam giác nối các đỉnh lại với nhau và tổng ba góc của tam giác luôn bằng 180 độ.

Tính Chất Của Tam Giác

Hình tam giác có nhiều tính chất quan trọng mà bạn cần ghi nhớ:

• Tổng các góc trong tam giác luôn bằng 180 độ.
• Định lý góc ngoài: Một góc ngoài của tam giác bằng tổng của hai góc trong không chứa nó.
• Bất đẳng thức tam giác: Tổng hai cạnh bất kỳ luôn lớn hơn cạnh còn lại.

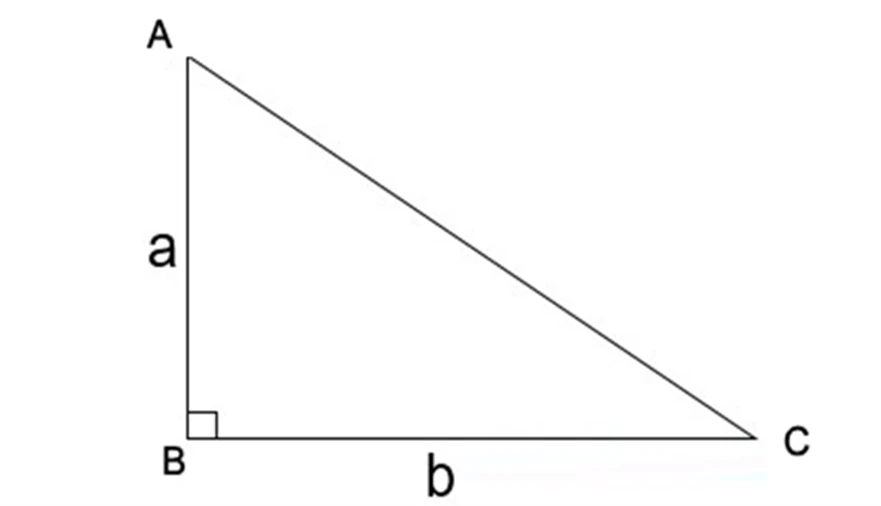
Công Thức Tính Diện Tích Tam Giác Khi Biết 3 Cạnh

Để tính diện tích tam giác khi biết 3 cạnh, chúng ta sẽ sử dụng công thức Heron. Công thức này rất hữu ích khi bạn không biết chiều cao của tam giác.

Công Thức Heron

Giả sử tam giác có ba cạnh `a`, `b` và `c`, nửa chu vi sẽ được tính như sau: \[ p = \frac{a + b + c}{2} \] Diện tích `S` của tam giác được tính bằng công thức Heron: \[ S = \sqrt{p \cdot (p - a) \cdot (p - b) \cdot (p - c)} \]

Ví Dụ Cách Tính Diện Tích Tam Giác Qua Công Thức Heron

Ví Dụ 1

Cho tam giác ABC có ba cạnh:

• AB = 7 cm
• AC = 8 cm
• BC = 9 cm

Bước 1: Tính nửa chu vi \[ p = \frac{7 + 8 + 9}{2} = 12 \text{ cm} \] Bước 2: Áp dụng công thức Heron \[ \begin{align*} S &= \sqrt{12 \cdot (12 - 7) \cdot (12 - 8) \cdot (12 - 9)} \\ &= \sqrt{12 \cdot 5 \cdot 4 \cdot 3} \\ &= \sqrt{720} = 26.83 \text{ cm²} \end{align*} \]

Một Số Lưu Ý Khi Tính Diện Tích Tam Giác

• Kiểm tra tính khả thi của tam giác: Trước khi áp dụng công thức Heron, hãy đảm bảo ba cạnh đã cho thỏa mãn bất đẳng thức tam giác.
• Sử dụng máy tính hoặc phần mềm hỗ trợ: Trong trường hợp bạn không quen với việc tính căn bậc hai, hãy sử dụng máy tính hoặc phần mềm hỗ trợ để có được kết quả chính xác.

Câu Hỏi Thường Gặp

1. Tại sao lại dùng công thức Heron?

Công thức Heron rất hữu ích khi bạn không có chiều cao của tam giác và chỉ biết độ dài ba cạnh.

2. Có cách nào khác để tính diện tích tam giác không?

Ngoài công thức Heron, bạn có thể tính diện tích tam giác nếu biết chiều cao và chiều dài của một cạnh bằng công thức cơ bản: \[ S = \frac{1}{2} \cdot a \cdot h \]

Tổng Kết

Tính diện tích tam giác khi biết ba cạnh là một kỹ năng quan trọng trong toán học. Việc hiểu và áp dụng công thức Heron sẽ giúp bạn giải quyết các bài toán kèm theo luận điểm hình học một cách dễ dàng hơn. Hãy thực hành với nhiều bài tập để làm quen và vững vàng hơn với kiến thức này! Chúc bạn thành công trong việc học toán và đạt điểm cao trong các kỳ thi!