Tính diện tích tam giác ABC dễ dàng và hiệu quả

Tính Diện Tích Tam Giác ABC: Hướng Dẫn Chi Tiết và Công Thức Dễ Hiểu Diện tích tam giác ABC là một trong những chủ đề cơ bản trong hình học mà học sinh cần nắm vững. Trong bài viết này, chúng tôi sẽ giúp bạn hiểu rõ về cách tính diện tích tam giác, cũng như các loại tam giác và công thức mà bạn có thể áp dụng. Bài viết được tổ chức theo trình tự logic với các tiêu đề phụ để dễ theo dõi.

1. Hình Tam Giác Là Gì?

Hình tam giác là hình có ba cạnh và ba đỉnh không nằm trên cùng một đường thẳng. Chúng ta thường gặp hình tam giác trong cuộc sống hàng ngày, từ các biểu tượng đơn giản cho đến các cấu trúc phức tạp. Hình tam giác không chỉ có nhiều ứng dụng trong thực tiễn mà còn mang lại nhiều kiến thức thú vị trong hình học.

1.1 Tính Chất Cơ Bản Của Tam Giác

Điểm nổi bật của tam giác bao gồm:

• Tổng các góc trong của tam giác luôn bằng 180 độ.
• Tính đối xứng: Tam giác có các tính chất đối xứng riêng theo từng loại.

2. Các Loại Hình Tam Giác

Có nhiều cách để phân loại tam giác dựa trên độ dài các cạnh và độ lớn các góc.

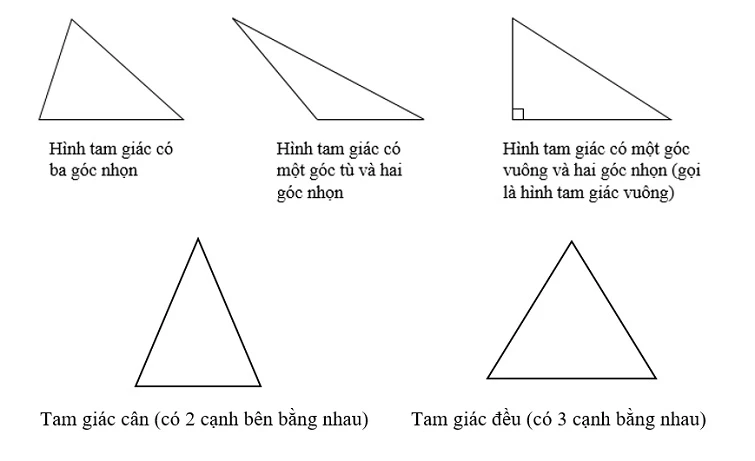
2.1 Phân Loại Theo Độ Dài Cạnh

• Tam Giác Cân: Có hai cạnh bằng nhau.
• Tam Giác Đều: Tất cả các cạnh đều bằng nhau.
• Tam Giác Thường: Tất cả các cạnh đều khác nhau.

2.2 Phân Loại Theo Độ Lớn Góc

• Tam Giác Vuông: Có một góc vuông 90 độ.
• Tam Giác Nhọn: Tất cả các góc đều nhỏ hơn 90 độ.
• Tam Giác Tù: Có một góc lớn hơn 90 độ.

3. Công Thức Tính Diện Tích Tam Giác

Dưới đây là các công thức tính diện tích tam giác bạn cần biết:

3.1 Công Thức Chung

Công thức tính diện tích tam giác là: \[ S = \frac{1}{2} \times \text{cạnh đáy} \times \text{chiều cao} \]

3.2 Các Trường Hợp Cụ Thể

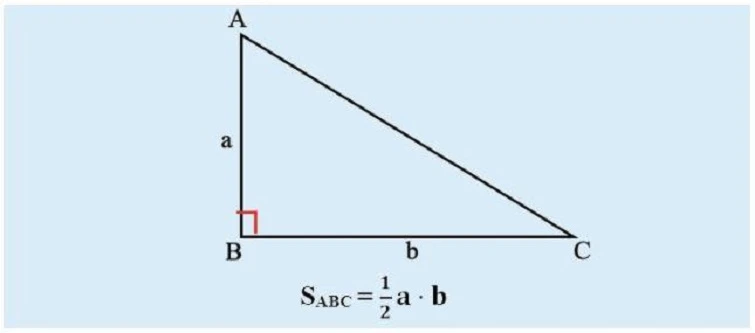
3.2.1 Tam Giác Vuông

Trong trường hợp tam giác vuông, công thức tính diện tích đơn giản như sau: \[ S = \frac{a \times b}{2} \] Trong đó:

• a và b là độ dài của hai cạnh góc vuông.

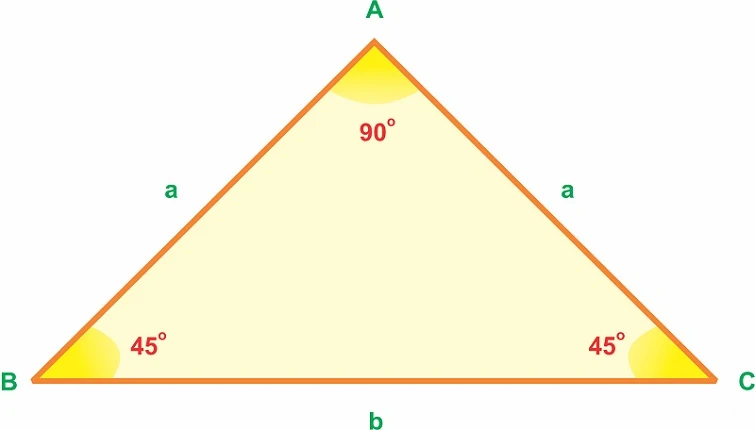
3.2.2 Tam Giác Cân

Đối với tam giác cân, công thức tính như sau: \[ S = \frac{1}{2} \times b \times h \] Trong đó:

• b là độ dài cạnh đáy
• h là chiều cao từ đỉnh xuống cạnh đáy.

3.2.3 Tam Giác Đều

Với tam giác đều, công thức tính diện tích có thể được biểu diễn dưới dạng: \[ S = \frac{a^2 \sqrt{3}}{4} \] Trong đó:

• a là độ dài cạnh tam giác.

3.2.4 Tam Giác Thường

Khi bạn biết độ dài ba cạnh của tam giác (a, b, c), bạn có thể sử dụng công thức Heron để tính diện tích:

• Tính nửa chu vi \( p = \frac{a + b + c}{2} \)
• Áp dụng công thức diện tích:

\[ S = \sqrt{p \times (p-a) \times (p-b) \times (p-c)} \]

4. Ví Dụ Minh Họa

Để giúp bạn hình dung rõ hơn, dưới đây là một số ví dụ minh họa.

4.1 Ví Dụ 1: Tính Diện Tích Tam Giác Vuông

Cho tam giác vuông có hai cạnh góc vuông lần lượt là 3 cm và 4 cm. Diện tích sẽ được tính như sau: \[ S = \frac{3 \times 4}{2} = 6 \text{ cm}^2 \]

4.2 Ví Dụ 2: Tính Diện Tích Tam Giác Cân

Cho tam giác cân với cạnh đáy là 6 cm và chiều cao là 4 cm. \[ S = \frac{1}{2} \times 6 \times 4 = 12 \text{ cm}^2 \]

4.3 Ví Dụ 3: Sử Dụng Công Thức Heron

Cho tam giác có ba cạnh a = 5 cm, b = 6 cm, c = 7 cm.

• Tính nửa chu vi:

\[ p = \frac{5 + 6 + 7}{2} = 9 \]

• Tính diện tích:

\[ S = \sqrt{9 \times (9-5) \times (9-6) \times (9-7)} = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} = 6\sqrt{6} \text{ cm}^2 \]

5. Câu Hỏi Thường Gặp

5.1 Làm Thế Nào Để Tính Diện Tích Tam Giác Biết Độ Dài Hai Cạnh Và Góc Giữa Chúng?

Khi biết độ dài hai cạnh và góc giữa, bạn có thể áp dụng công thức: \[ S = \frac{1}{2} \times a \times b \times \sin(C) \] Trong đó \( a \) và \( b \) là độ dài cạnh và \( C \) là góc giữa.

5.2 Có Công Thức Nào Để Tính Diện Tích Tam Giác Trong Hệ Tọa Độ?

Trong không gian tọa độ Oxyz, bạn có thể sử dụng công thức sau: \[ S = \frac{1}{2} |[AB;AC]| \] Trong đó \( AB \) và \( AC \) là các vector đại diện cho các cạnh của tam giác.

6. Tóm Tắt

Việc tính diện tích tam giác là một kỹ năng cơ bản trong toán học, và nó sẽ giúp ích rất nhiều cho bạn trong học tập. Thông qua các công thức cụ thể và ví dụ minh họa, chúng tôi hy vọng bạn đã nắm vững cách tính diện tích tam giác. Hãy thường xuyên luyện tập để cải thiện kỹ năng của mình!