Cách Tính Diện Tích Hình Tròn Chính Xác Nhất

Tìm hiểu về tính diện tích hình tròn

Hình tròn, một trong những hình học cơ bản và phổ biến nhất trong cuộc sống hàng ngày, không chỉ xuất hiện trong nhiều lĩnh vực học thuật mà còn nằm trong thiết kế, xây dựng hay nghệ thuật. Để có thể tính được diện tích của hình tròn một cách chính xác, việc nắm vững công thức và cách áp dụng là rất cần thiết. Bài viết này sẽ giúp bạn đọc hiểu rõ hơn về công thức tính diện tích hình tròn, cách sử dụng nó trong các bài tập và thực tiễn.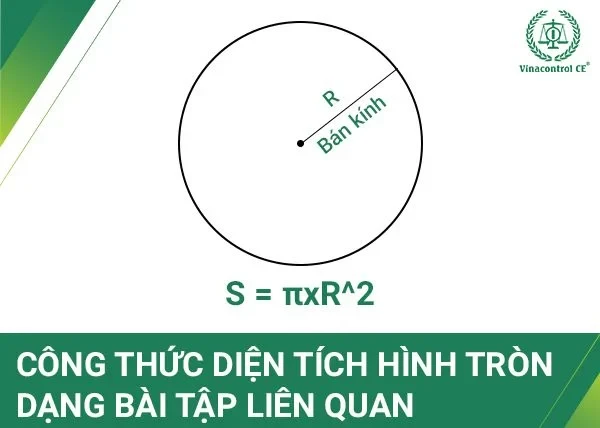

1. Công thức tính diện tích hình tròn

Diện tích của hình tròn được xác định bằng diện tích nằm bên trong đường tròn và được phát biểu như sau: diện tích hình tròn tỷ lệ thuận với bình phương bán kính của nó. Cụ thể, công thức tính diện tích hình tròn được diễn tả như sau:

• S = πR²

Ở đây:

• S: là diện tích hình tròn.
• π: là số PI, có giá trị xấp xỉ 3,14.
• R: là bán kính hình tròn.

Tính chất của hình tròn

Trước khi đi vào ứng dụng công thức, chúng ta cần biết một số tính chất cơ bản của hình tròn:

• Tâm: Điểm trung tâm của hình tròn, ký hiệu là "O".
• Bán kính (R): Khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn.
• Đường kính (D): Đoạn thẳng nối hai điểm trên đường tròn và đi qua tâm, bằng hai lần bán kính (D = 2R).

2. Cách giải bài tập về diện tích hình tròn

Hãy cùng xem xét một số dạng bài tập thường gặp liên quan đến diện tích hình tròn cũng như cách giải quyết chúng hiệu quả.

2.1 So sánh diện tích hai hình tròn

Trong dạng bài tập này, bạn cần tính diện tích của hai hình tròn và thực hiện phép so sánh. Lưu ý rằng:

• Cần quy đổi đơn vị diện tích của hai hình tròn về cùng một đơn vị nếu đề bài cho dữ liệu khác nhau.
• Tương tự với bán kính, bạn cũng nên quy đổi về cùng một đơn vị đo trước khi so sánh.

Ví dụ: So sánh diện tích hai hình tròn với dữ liệu

• Hình tròn S1 có diện tích 10 cm².
• Hình tròn S2 có diện tích 1200 mm².

Giải: Quy đổi diện tích S2 sang cm²: 1200 mm² = 12 cm². Vậy S2 > S1. Hình tròn S2 có diện tích lớn hơn so với hình S1.

2.2 Tính diện tích hình tròn khi biết bán kính hoặc đường kính

Nếu đề bài cho biết bán kính, bạn chỉ cần áp dụng công thức S = πR². Nếu cho biết đường kính, bạn cần chuyển đổi nó thành bán kính bằng công thức R = D/2 trước khi tính diện tích. Ví dụ: Cho hình tròn C có đường kính D = 20 cm. Hãy tính S hình tròn C? Giải:

• Bán kính R = D/2 = 20/2 = 10 cm.
• S hình tròn C: S = πR² = 3,14 * 10² = 314 cm².

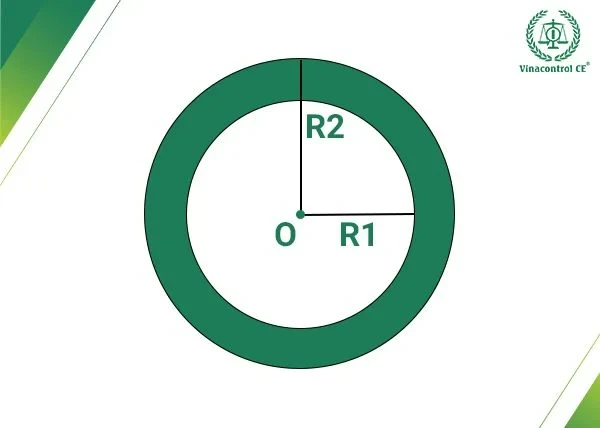
2.3 Tính diện tích hình vành khăn

Khi có một hình tròn lớn và một hình tròn nhỏ bên trong, bạn cần tính diện tích hình vành khăn bằng cách lấy diện tích lớn trừ diện tích nhỏ. Ví dụ: Biết R1 = 10 cm (hình tròn nhỏ) và R2 = 20 cm (hình tròn lớn). Giải:

• Diện tích hình tròn nhỏ: S1 = πR1² = 3,14 * 10² = 314 cm².
• Diện tích hình tròn lớn: S2 = πR2² = 3,14 * 20² = 1256 cm².
• Diện tích hình vành khăn = S2 - S1 = 1256 - 314 = 942 cm².

3. Bài tập tự luyện tại nhà

Sau khi đã hiểu rõ các công thức và cách giải, bạn có thể thử sức với những bài tập sau:

• Tính chu vi hình tròn có:

- a, d = 3 cm. - b, d = 4.5 m.

• Tính diện tích hình tròn có:

- a, r = 5 cm. - b, r = 3.3 m.

• Một sợi dây thép hình tròn có bán kính 7 cm. Tính chiều dài dây thép đó.
• Tính diện tích hình tròn với:

- a, r = 5 cm. - b, d = 12 dm.

• Giếng nước có miệng hình tròn đường kính 1.6 m, xung quanh có thành rộng 0.3 m. Tính diện tích thành giếng.
• Bồn hoa hình tròn có đường kính 40 cm. Bồn hoa khác có chu vi 9.42 m. Hỏi bồn nào có diện tích lớn hơn?

Kết luận

Qua bài viết này, bạn đã được trang bị kiến thức về công thức tính diện tích hình tròn và các dạng bài tập liên quan. Hãy luyện tập nhiều hơn để củng cố kỹ năng và khả năng giải quyết bài tập hình học nhé! Viện đào tạo Vinacontrol hy vọng bạn sẽ áp dụng được những kiến thức này vào học tập và cuộc sống thực tiễn.