Hướng Dẫn Tính Diện Tích Hình Thang Đơn Giản

Hình thang là một trong những hình dạng cơ bản trong hình học, với những ứng dụng thú vị trong cuộc sống cũng như trong các bài toán học. Biết cách tính diện tích hình thang là kiến thức cần thiết không chỉ cho học sinh mà còn cho những ai làm việc trong lĩnh vực liên quan đến kiến trúc, thiết kế và nhiều lĩnh vực khác. Trong bài viết này, chúng ta sẽ khám phá các công thức tính diện tích hình thang, cũng như các bài toán minh họa và cách áp dụng công thức trong thực tế.

1. Công Thức Tính Diện Tích Hình Thang

1.1. Định Nghĩa Hình Thang

Hình thang là một tứ giác có hai cạnh song song với nhau, được gọi là các cạnh đáy. Các cạnh còn lại được gọi là cạnh bên. Để tính diện tích hình thang, bạn cần biết độ dài của hai cạnh đáy và chiều cao h.

1.2. Công Thức Chung

Diện tích hình thang có thể được tính bằng công thức: \[ S = \frac{(a + b)}{2} \times h \] Trong đó:

• S: Diện tích hình thang
• a và b: Độ dài của hai cạnh đáy
• h: Chiều cao hạ từ cạnh đáy a xuống b hoặc ngược lại (khoảng cách giữa 2 cạnh đáy)

Hình minh họa:

1.3. Bài Thơ Ghi Nhớ

Có một cách ghi nhớ khá dễ dàng với một bài thơ về cách tính diện tích hình thang:

Muốn tính diện tích hình thang

Đáy lớn đáy nhỏ ta đem cộng vào

Cộng vào nhân với chiều cao

Chia đôi lấy nửa thế nào cũng ra

2. Công Thức Tính Diện Tích Hình Thang Khi Biết 4 Cạnh

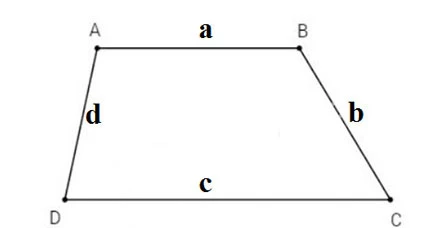
2.1. Bài Toán Nâng Cao

Khi đề bài cho biết độ dài của 4 cạnh (gọi là a, b, c, d), trong đó a và c là cạnh đáy, b và d là cạnh bên, thì bạn có thể tính diện tích hình thang bằng công thức hơi phức tạp hơn: \[ S = \frac{(a + c)}{2} \times h \]

2.2. Chiều Cao Hình Thang

Bạn có thể tính chiều cao h bằng cách sử dụng công thức Pythagore nếu biết độ dài các cạnh bên.

3. Tính Diện Tích Hình Thang Vuông

3.1. Định Nghĩa

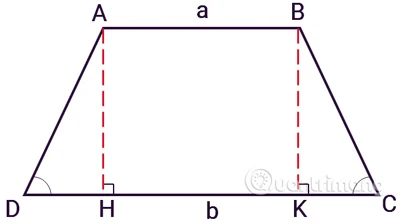
Hình thang vuông là hình thang có một góc vuông, và chiều cao h chính là cạnh bên vuông góc với hai đáy.

3.2. Công Thức Tính

Diện tích hình thang vuông cũng được tính bằng công thức: \[ S = \frac{(a + b)}{2} \times h \]

Hình minh họa:

4. Tính Diện Tích Hình Thang Cân

4.1. Đặc Điểm Hình Thang Cân

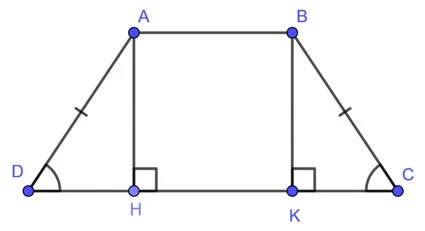
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau và 2 cạnh bên bằng nhau.

4.2. Phương Pháp Tính

Để tính diện tích hình thang cân, bên cạnh áp dụng công thức diện tích hình thang chung, bạn có thể chia nhỏ hình thang thành hình chữ nhật và hai hình tam giác để tính diện tích từng phần rồi ghép lại.

Hình minh họa:

5. Tính Độ Dài Cạnh Đáy Hình Thang

Khi biết diện tích, chiều cao và độ dài một cạnh đáy, bạn có thể tìm được độ dài cạnh còn lại bằng công thức sau: \[ AB = 2 \times \frac{S_{ABCD}}{h} - CD \]

6. Các Dạng Toán Tính Diện Tích Hình Thang

6.1. Ví Dụ 1: Tính Diện Tích Hình Thang

Đề bài: Tính diện tích hình thang biết độ dài hai đáy lần lượt là 18 cm và 14 cm; chiều cao là 9 cm. Giải: Áp dụng công thức, ta có: \[ S = \frac{(18 + 14)}{2} \times 9 = 144 \text{ cm}^2 \] Vậy diện tích hình thang là 144 cm².

6.2. Ví Dụ 2: Hình Thang Có Thay Đổi

Đề bài: Có một mảnh đất hình thang với đáy bé là 24 m, đáy lớn là 30 m. Mở rộng hai đáy về phía bên phải của mảnh đất với đáy lớn thêm 7 m, đáy nhỏ thêm 5 m, thu được mảnh đất hình thang mới với diện tích lớn hơn diện tích ban đầu là 36 m². Tính diện tích mảnh đất hình thang ban đầu. Giải: Diện tích tăng thêm là diện tích hình thang với đáy lớn 7 m và đáy nhỏ 5 m: Chiều cao mảnh đất hình thang ban đầu được tính như sau: \[ h = \frac{36 \times 2}{7 + 5} = 6 \text{ m} \] Diện tích mảnh đất ban đầu là: \[ S = 6 \times \frac{(24 + 30)}{2} = 162 \text{ m}² \]

6.3. Ví Dụ 3: Tính Đáy Hình Thang Vuông

Đề bài: Cho hình thang vuông có khoảng cách hai đáy là 16 cm, đáy nhỏ bằng ¾ đáy lớn. Tính độ dài hai đáy khi biết diện tích hình thang vuông là 112 cm². Giải: Tổng độ dài hai đáy là: \[ (112 \times 2) / 16 = 14 \text{ cm} \] Gọi độ dài đáy bé là a, còn đáy lớn là b, theo đó ta có:

• a + b = 14
• a = \( \frac{3}{4} b \)

Giải hệ phương trình, bạn sẽ tìm được độ dài hai đáy.

6.4. Ví Dụ 4: Hình Thang Cân

Đề bài: Hình thang cân ABCD (AB // CD) có AB = 5 cm, CD = 13 cm, AD = 5 cm. Tính diện tích hình thang ABCD? Giải: Gọi AH, BK là hai đường cao của hình thang. Tính chiều cao AH bằng định lý Pythagore.

• Tính DH:

\[ DH = KC = \frac{(CD - AB)}{2} = \frac{(13 - 5)}{2} = 4 \text{ cm} \]

• Áp dụng định lý Pythagore vào tam giác vuông AHD:

\[ AH² = AD² - DH² \to AH² = 5² - 4² = 9 \Rightarrow AH = 3 \text{ cm} \]

• Vậy diện tích hình thang ABCD là:

\[ S = AH \times \frac{(AB + CD)}{2} = 3 \times \frac{(5 + 13)}{2} = 24 \text{ cm}² \]

Kết Luận

Như vậy, bài viết đã trình bày đầy đủ công thức và cách tính diện tích hình thang, cũng như là các dạng bài toán minh họa. Từ những kiến thức này, bạn có thể ứng dụng vào các tình huống thực tế và giải các bài toán phức tạp hơn. Hãy cùng vận dụng và thực hành để trở thành người tính toán giỏi hơn!