Tìm hiểu về nguyên hàm và ứng dụng trong toán học

Trong chương trình Toán 12, nguyên hàm là một trong những phần kiến thức quan trọng. Việc nắm vững lý thuyết và các công thức liên quan đến nguyên hàm không chỉ giúp các bạn học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng giúp làm tốt các đề thi THPT Quốc gia. Hãy cùng VUIHOC khám phá một cách chi tiết về nguyên hàm và các công thức hữu ích để chinh phục phần kiến thức này.

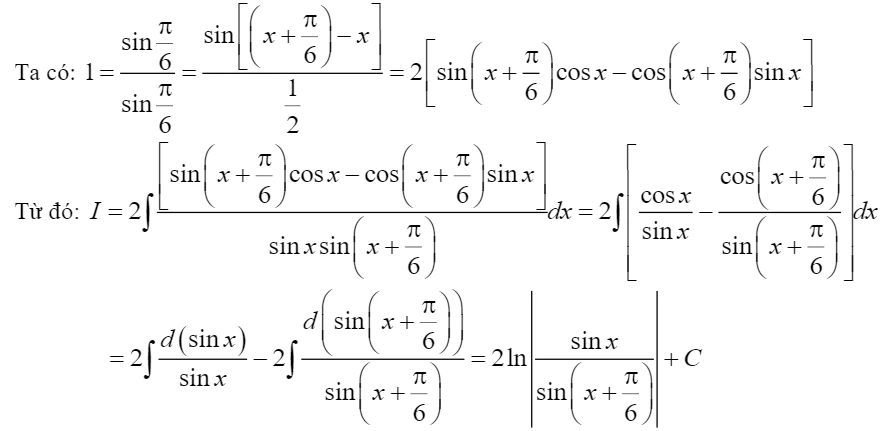
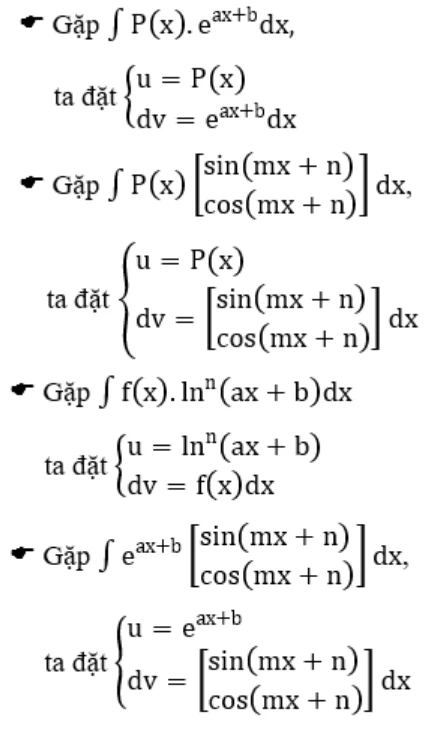
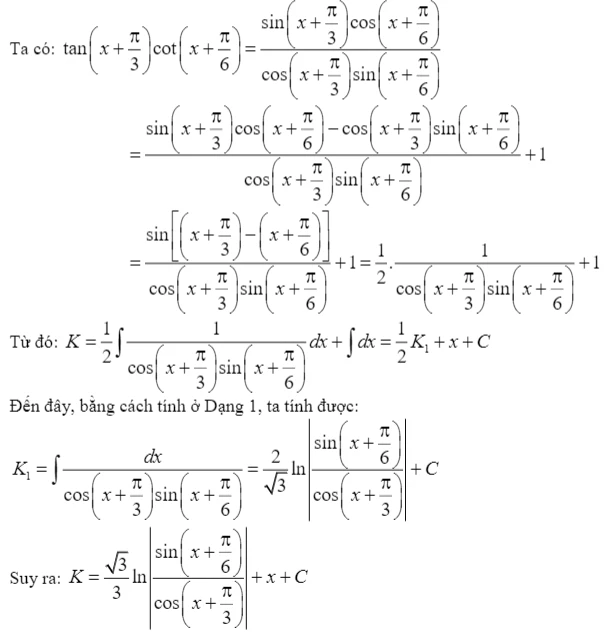
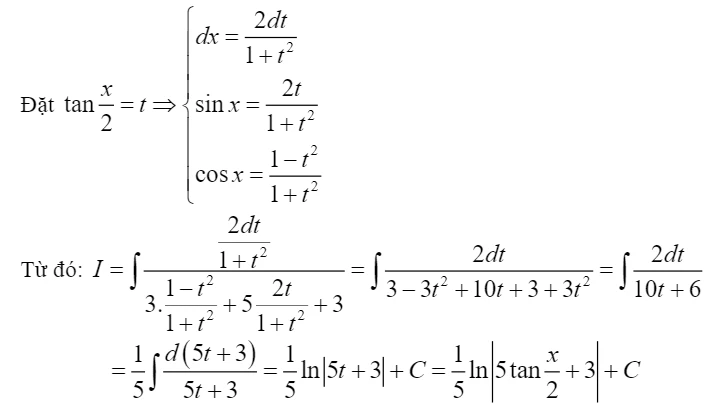
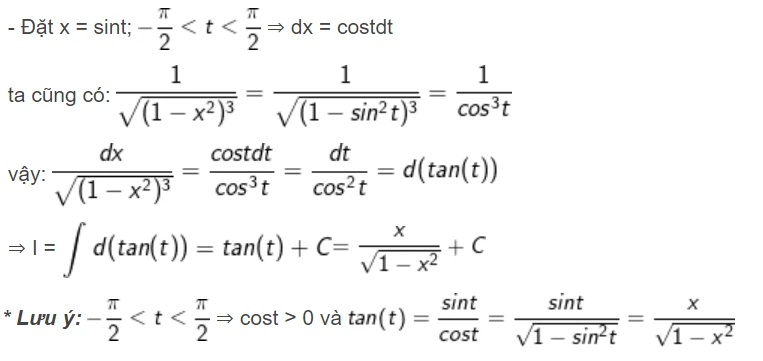
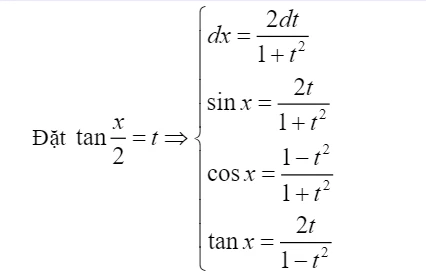
1. Lý thuyết Nguyên Hàm

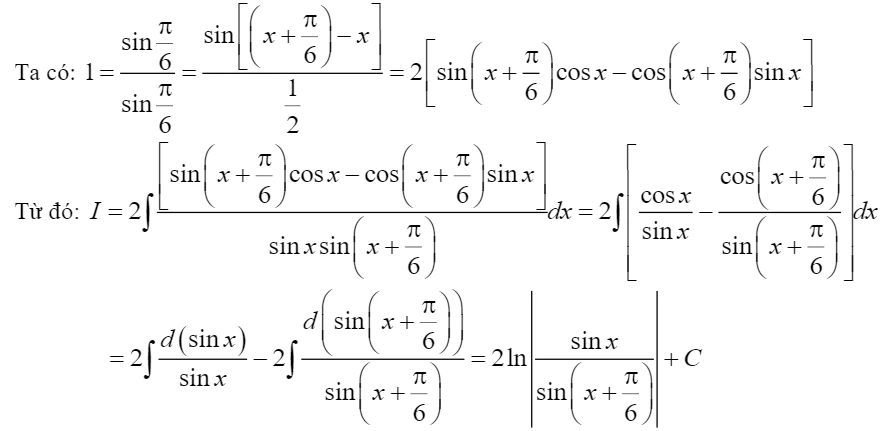
1.1. Định nghĩa Nguyên Hàm là gì?

Nguyên hàm của một hàm số thực được định nghĩa là một hàm số mà khi lấy đạo hàm sẽ bằng hàm số ban đầu. Cụ thể, cho hàm số f xác định trên K, một nguyên hàm của f trên K là một hàm F thoả mãn: \[ F’(x) = f(x) \] với \( x \in K \). Ví dụ: Với hàm số \( f(x) = \cos x \), ta có nguyên hàm: \[ F(x) = \sin x \] vì \( (\sin x)’ = \cos x \).

1.2. Tính chất của Nguyên Hàm

Nguyên hàm có một số tính chất chính như sau:

• Tính tuyến tính:

\[ \int [f(x) + g(x)]dx = \int f(x)dx + \int g(x)dx \]

• Tính chất của hệ số:

\[ \int kf(x)dx = k\int f(x)dx \quad (với \, k \, là \, số \, thực) \] Ví dụ: Tính nguyên hàm của hàm số \( \sin^2 x \): \[ \int \sin^2 x \, dx = \int \frac{1 - \cos 2x}{2} \, dx = \frac{1}{2}\int dx - \frac{1}{2}\int \cos 2x \, dx = \frac{x}{2} - \frac{\sin 2x}{4} + C \]

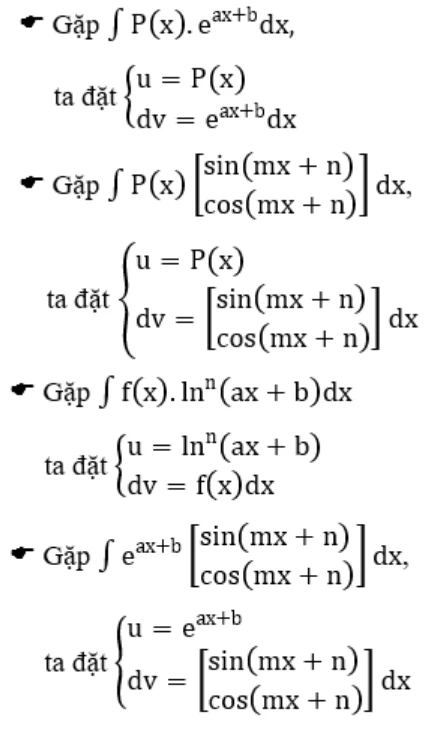
2. Tổng hợp đầy đủ các công thức Nguyên Hàm dành cho học sinh lớp 12

2.1. Bảng công thức Nguyên Hàm cơ bản

Dưới đây là bảng tổng hợp các công thức nguyên hàm cơ bản cần nhớ trong chương trình Toán 12:

• \( \int x^n dx = \frac{x^{n+1}}{n+1} + C, n \neq -1 \)
• \( \int e^x dx = e^x + C \)
• \( \int \ln x \, dx = x \ln x - x + C \)

2.2. Bảng công thức Nguyên Hàm nâng cao

Ngoài các công thức cơ bản, còn có nhiều công thức nguyên hàm nâng cao mà các bạn cần biết để giải quyết các bài toán khó hơn.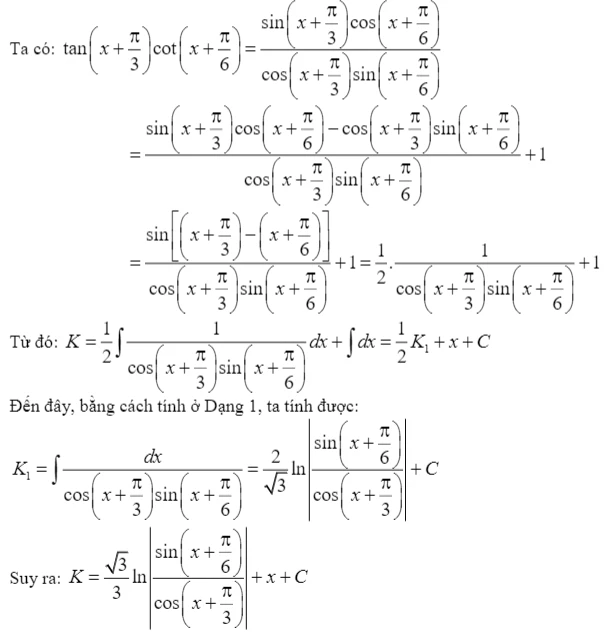

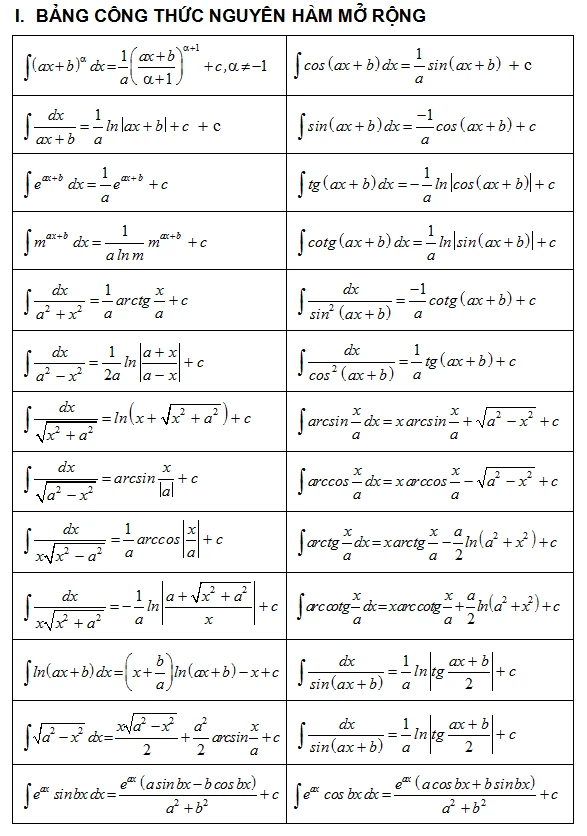
2.3. Bảng công thức Nguyên Hàm mở rộng

Các công thức nguyên hàm mở rộng hỗ trợ giải quyết bài toán khó hơn và cụ thể hơn về từng loại hàm như hàm lượng giác, hàm mũ...

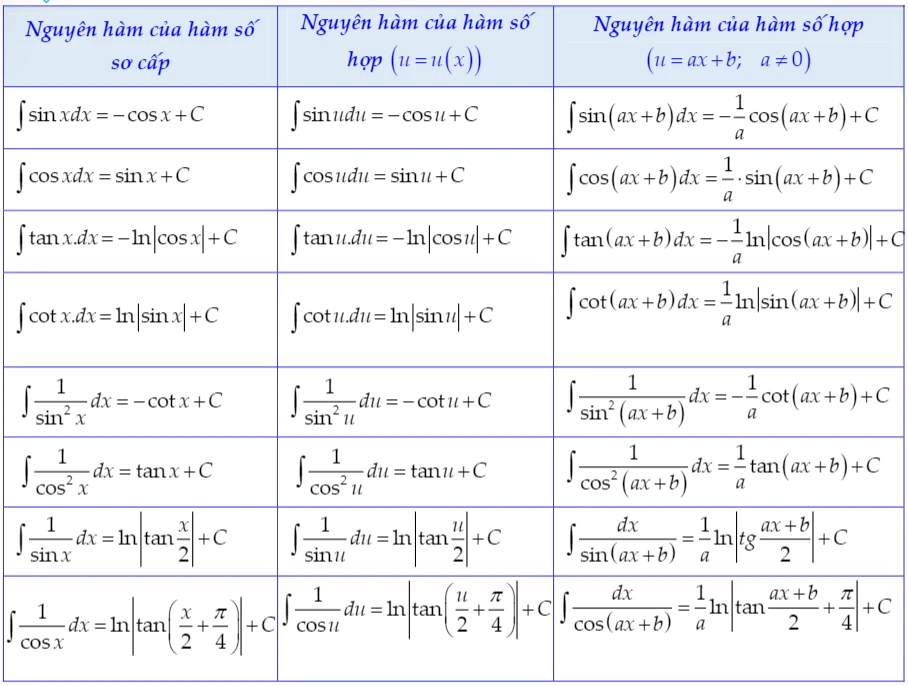
3. Bảng công thức Nguyên Hàm lượng giác

Nguyên hàm của các hàm lượng giác thường gặp, bao gồm:

• \( \int \sin x \, dx = -\cos x + C \)
• \( \int \cos x \, dx = \sin x + C \)

Bảng công thức này rất hữu ích trong việc giải các bài tập có liên quan đến hàm lượng giác.

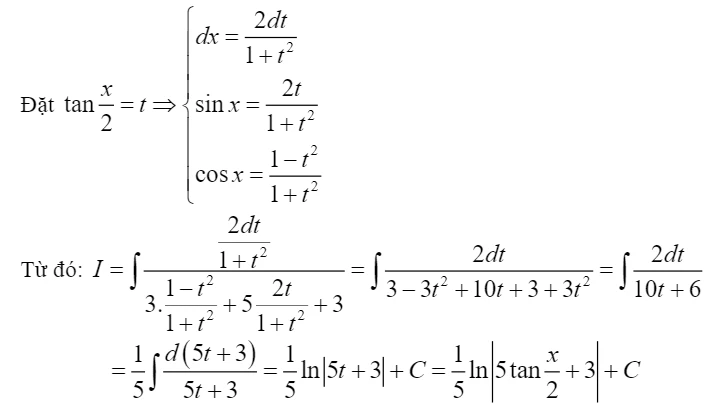
4. Các phương pháp Tính Nguyên Hàm nhanh nhất và bài tập từ cơ bản đến nâng cao

Để đạt được hiệu quả cao trong việc tính nguyên hàm, học sinh có thể áp dụng một số phương pháp sau:

4.1. Công thức Nguyên Hàm từng phần

Phương pháp này dựa trên định lý cơ bản: \[ \int u \, dv = uv - \int v \, du \] Ví dụ: Tính nguyên hàm của \( \int x \sin x \, dx \).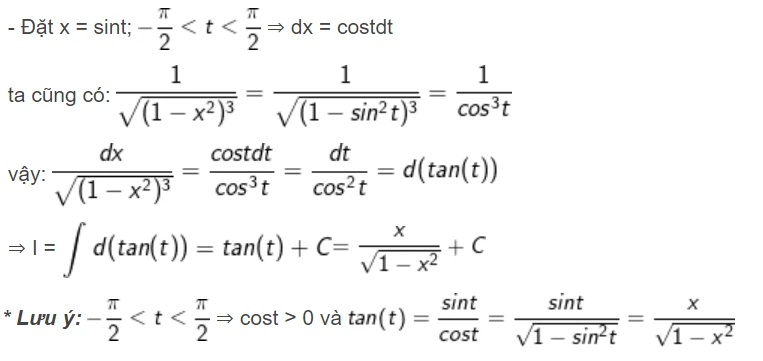

4.2. Phương pháp tính Nguyên Hàm hàm số lượng giác

Một số dạng thường gặp:

• \( I=\int \frac{dx}{\sin(x+a) \sin(x+b)} \)
• \( K=\int \tan(x+a) \tan(x+b) \, dx \)

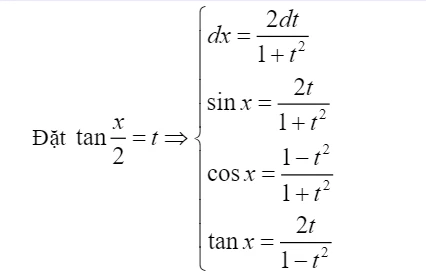
4.3. Cách tính Nguyên Hàm của hàm số mũ

Cần nắm vững bảng nguyên hàm của các hàm số mũ cơ bản, ví dụ:

• \( \int e^{kx} \, dx = \frac{1}{k}e^{kx} + C \)

4.4. Phương pháp Nguyên hàm đặt ẩn phụ

Khi gặp các hàm khó tính, việc đặt ẩn phụ có thể làm đơn giản hóa bài toán. Ví dụ: Tìm nguyên hàm \( I=\int \frac{dx}{\sqrt{(1-x^2)^3}} \).

5. Kết thúc

Việc ôn tập và thực hành các công thức nguyên hàm là rất cần thiết để học sinh có thể thành thạo phần kiến thức này. Ngoài lý thuyết và công thức, các em cần thường xuyên làm bài tập để củng cố kiến thức và kỹ năng. Hy vọng bài viết này sẽ giúp các em có thêm tài liệu tham khảo cho việc ôn tập và làm bài tập về nguyên hàm tốt hơn. Xem thêm:

• Công thức nguyên hàm ln và cách giải các dạng bài tập
• Tính nguyên hàm của tanx bằng công thức cực hay
• Phương pháp tính tích phân từng phần và ví dụ minh họa

Hãy đến với VUIHOC để được học tập và ôn luyện những kiến thức toán học bổ ích khác nhé!