Hướng Dẫn Tính Thể Tích Khối Chóp Đầy Đủ Chi Tiết

Trong chương trình học hình học lớp 12, thể tích khối chóp là một trong những chủ đề quan trọng thường xuyên xuất hiện trong các đề thi Đại học. Kỹ năng tính thể tích khối chóp không chỉ giúp các bạn học sinh nắm vững kiến thức, mà còn nâng cao khả năng tư duy toán học. Bài viết này sẽ hướng dẫn chi tiết về cách tính thể tích khối chóp, cùng với các công thức và ví dụ cụ thể để bạn dễ dàng hiểu và áp dụng.

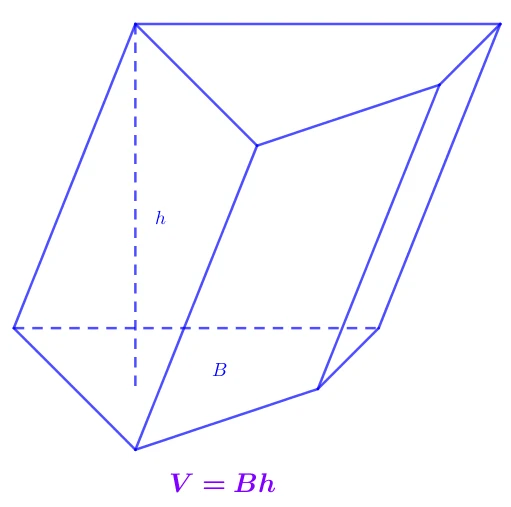
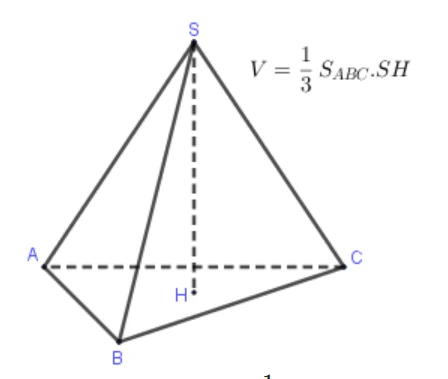
1. Ôn Tập Lý Thuyết Thể Tích Khối Chóp

Thể tích khối chóp được định nghĩa là lượng không gian mà khối chóp đó chiếm. Đơn vị đo thể tích thường là cm³ (centimeter cube).

1.1 Định Nghĩa Khối Chóp

Khối chóp là một hình không gian có một đỉnh gọi là đỉnh chóp và một mặt đáy là một đa giác bất kỳ. Tất cả các điểm trên mặt đáy đều kết nối với đỉnh chóp bằng các đoạn thẳng.

1.2 Công Thức Tính Thể Tích Khối Chóp

Công thức tính thể tích khối chóp được xác định bằng công thức: \[ V = \frac{1}{3} S h \]

• Trong đó:

- \( S \) là diện tích đáy - \( h \) là chiều cao từ đỉnh chóp đến mặt phẳng đáy

1.3 Một Số Công Thức Khác

Ngoài công thức trên, còn có các trường hợp đặc biệt như tính thể tích của khối chóp tam giác, khối chóp lục giác đều, khối chóp tròn xoay... Trong bài viết này, chúng ta sẽ trình bày 12 công thức thường gặp và dễ áp dụng nhất.

2. Các Công Thức Tính Thể Tích Khối Chóp Dễ Hiểu Nhất

Dưới đây là các công thức và cách tính thể tích của các loại khối chóp đa dạng mà bạn có thể gặp trong các bài kiểm tra.

2.1 Cách Tính Thể Tích Khối Chóp Có Mặt Bên Vuông Góc Đáy

Để sử dụng công thức này, cần nắm vững đặc điểm của hình chóp. Nếu trong khối chóp có hai mặt bên cùng vuông góc với đáy thì chiều cao của khối chóp được xác định là giao tuyến của hai mặt bên đó. Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, với các cạnh tiếp giáp lần lượt là BA = 3a, BC = 4a. Tính thể tích khối chóp S.ABC.

2.2 Phương Pháp Tính Thể Tích Khối Chóp Lồi Có Cạnh Bên Vuông Góc Đáy

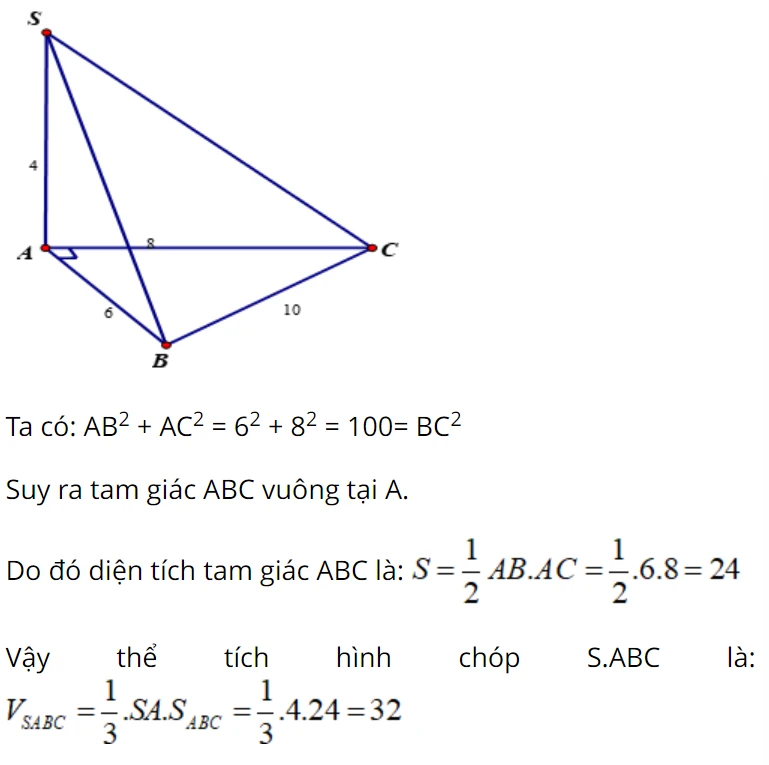
Với khối chóp mà các cạnh bên đều vuông góc với đáy, chiều cao của chóp chính là khoảng cách từ đỉnh chóp đến đáy. Ví dụ: Cho khối chóp S.ABC có SA vuông góc với đáy, SA= 4, AB= 6, BC= 10 và CA= 8. Tính thể tích khối chóp S.ABC.

2.3 Thể Tích Khối Chóp Với Đáy Hình Vuông

Đối với khối chóp có đáy là hình vuông, ta có: Công thức: \[ V = \frac{1}{3} a^2 h \] Ví dụ: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a và chiều cao h.

2.4 Tìm Thể Tích Khối Chóp Lập Phương

Khối chóp lập phương là một dạng khối chóp mà tất cả các mặt đều là hình vuông. Thể tích của chúng rất đơn giản. Công thức: \[ V = a^3 \]

2.5 Thể Tích Khối Chóp Lăng Trụ Tam Giác Đều

Điều thú vị là khi đáy hình chóp là một tam giác đều mà chiều cao cũng được cho trước. Ví dụ: Tính thể tích hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a và chiều cao h.

2.6 Cách Tính Thể Tích Khối Chóp Lục Giác Đều

• Công thức:

\[ V = \frac{1}{3} S_{ABCDEF} \cdot SO \]

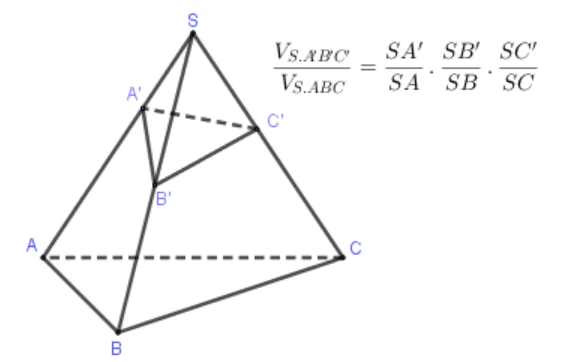
2.7 Tính Thể Tích Khối Chóp Khi Biết 3 Cạnh Bên

Propeties: Tính thể tích của khối tứ diện bằng các cạnh.

• Công thức:

\[ V = \frac{1}{12} \sqrt{a^2 b^2 c^2 + d^2 e^2 f^2 + g^2 h^2 i^2 - a^2 d^2 - b^2 e^2 - c^2 f^2} \]

2.8 Tìm Thể Tích Bằng Cách Giải Ba Cạnh Đối Đỉnh

Cách giải: Sử dụng các cạnh của khối chóp theo công thức: \[ V = \frac{1}{6} a b c \]

2.9 Thể Tích Khối Chóp Tròn Xoay

• Công thức:

\[ V = \frac{1}{3} \pi r^2 h \]

2.10 Tính Thể Tích Khối Chóp Tam Giác Đều

• Công thức:

\[ V = \frac{1}{6} a^2 h \]

2.11 Tính Thể Tích Khối Chóp Tứ Giác Đều Cạnh Đáy Bằng a

• Công thức:

\[ V = \frac{1}{3} \cdot a^2 \cdot \frac{a\sqrt{3}}{2} = \frac{a^3\sqrt{3}}{6} \]

2.12 Tổng Quan Ôn Tập Lý Thuyết

Tổng kết lại, để có thể thành thạo trong việc tính thể tích khối chóp, việc nắm vững lý thuyết và các công thức là cần thiết.

Kết Luận

Hy vọng bài viết này giúp ích cho các em trong việc ôn tập kiến thức hình học về thể tích khối chóp. Nắm vững lý thuyết và thực hành nhiều bài tập sẽ giúp các em có được kết quả tốt trong kỳ thi THPT sắp tới. Hãy tiếp tục theo dõi VUIHOC để nhận thêm nhiều kiến thức hữu ích khác! Xem thêm:

• Tổng hợp công thức toán hình 12
• Cách học hình học không gian tốt - toán 12
• Công thức tính thể tích khối cầu nhanh và chính xác nhất