Tìm hiểu trực tâm của tam giác và tính chất của nó

Trực tâm của tam giác là một trong những khái niệm cơ bản và quan trọng trong hình học. Nó không chỉ là một điểm đặc biệt của tam giác mà còn đóng vai trò lớn trong việc giải quyết các bài toán hình học liên quan đến tam giác. Bài viết này sẽ giúp bạn hiểu rõ hơn về trực tâm của tam giác, từ khái niệm, tính chất đến cách xác định trực tâm và bài tập thực hành.

1. Trực Tâm Là Gì?

1.1 Khái Niệm

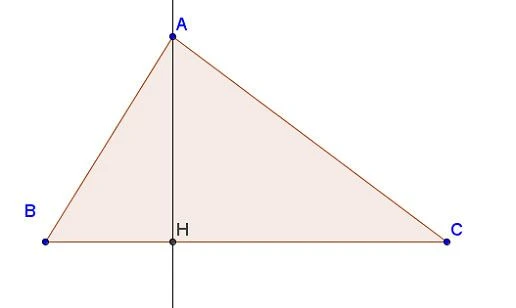
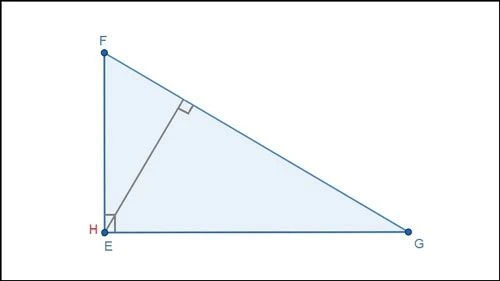
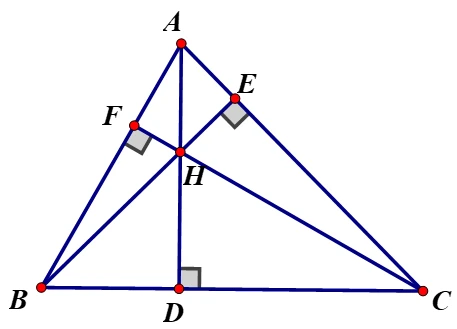
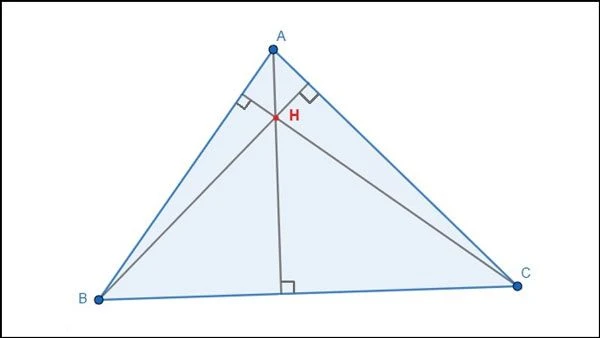
Trực tâm (hay còn gọi là "hội tụ của các đường cao") của một tam giác là điểm giao nhau của ba đường cao của tam giác. Đường cao được xác định bằng cách kẻ một đoạn thẳng từ một đỉnh của tam giác vuông góc với cạnh đối diện của nó. Mỗi tam giác có ba đường cao và điểm giao nhau của chúng là trực tâm.

1.2 Ý Nghĩa Trong Hình Học

Trực tâm không chỉ đơn thuần là điểm giao nhau của ba đường cao. Nó còn có những tính chất đặc biệt giúp ích cho việc giải quyết các bài toán hình học, chẳng hạn như:

• Giúp xác định các mối quan hệ giữa các điểm trong tam giác.
• Hỗ trợ lúc được chiếu xuống các đường thẳng song song hay xây dựng các hình hình học phức tạp hơn.

2. Đường Cao Của Một Tam Giác

2.1 Định Nghĩa Đường Cao

Đường cao trong một tam giác được định nghĩa rõ ràng là đoạn thẳng kẻ từ một đỉnh vuông góc với đường thẳng chứa cạnh đối diện. Mỗi tam giác luôn có chính xác ba đường cao.

2.2 Minh Họa Đường Cao

Hãy xem xét tam giác ABC. Để tìm đường cao từ đỉnh A, chúng ta kẻ một đường thẳng từ A đến đường thẳng chứa cạnh BC. Tương tự, với các đỉnh B và C, ta có các đoạn vuông góc lần lượt đến hai cạnh còn lại.

3. Tính Chất Của Trực Tâm Trong Tam Giác

3.1 Đặc Điểm Của Trực Tâm

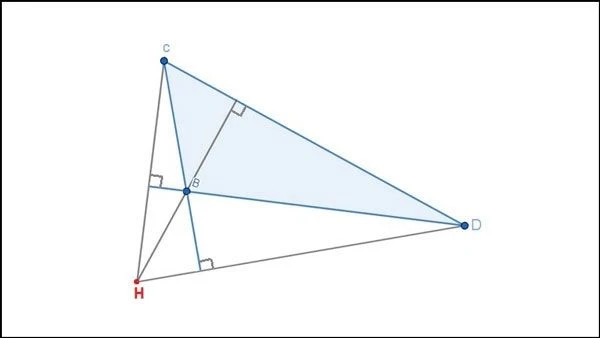
• Điểm Giao Nhau: Trực tâm là điểm đồng quy của ba đường cao.
• Vị Trí Đặc Biệt:

- Trực tâm của tam giác nhọn nằm trong tam giác. - Trực tâm của tam giác vuông trùng với đỉnh góc vuông. - Trực tâm của tam giác tù nằm bên ngoài tam giác.

3.2 Tính Chất Quan Trọng Khác

• Trực tâm là tâm của đường tròn ngoại tiếp tam giác.
• Tại trực tâm, tổng độ dài của đoạn thẳng từ trực tâm đến ba đỉnh của tam giác là nhỏ nhất so với bất kỳ điểm nào khác trong tam giác.

4. Cách Xác Định Trực Tâm Của Tam Giác

4.1 Đối Với Tam Giác Nhọn

Để xác định trực tâm của một tam giác nhọn:

• Kẻ hai đường cao từ hai đỉnh của tam giác đến cạnh đối diện.
• Điểm giao nhau của hai đường cao ấy chính là trực tâm.

4.2 Đối Với Tam Giác Vuông

Trong trường hợp tam giác vuông:

• Trực tâm sẽ trùng với đỉnh góc vuông. Bạn không cần phải kẻ thêm đường cao.

4.3 Đối Với Tam Giác Tù

Đối với tam giác tù:

• Kẻ hai đường cao từ hai đỉnh đến cạnh đối diện.
• Để xác định trực tâm, bạn cần vẽ thêm đường cao từ điểm đỉnh góc tù xuống cạnh đối diện.

5. Ví Dụ Minh Họa

Để giúp cho việc hiểu rõ hơn, dưới đây là những ví dụ minh họa cụ thể.

5.1 Ví Dụ 1: Tam Giác Nhọn

Giả sử bạn có tam giác ABC với ba đỉnh A, B và C. Kẻ đường cao từ A đến BC và từ B đến AC. Điểm giao nhau của hai đường cao này là trực tâm H.

5.2 Ví Dụ 2: Tam Giác Vuông

Xét tam giác ABC, trong đó A là đỉnh vuông. Trực tâm H trùng với A.

5.3 Ví Dụ 3: Tam Giác Tù

Xét tam giác ABC có góc A tù. Bạn kẻ đường cao từ B và C. Điểm giao nhau chính là trực tâm H.

6. Bài Tập Thực Hành Có Đáp Án

6.1 Bài Tập Trắc Nghiệm

Câu 1: Cho tam giác ABC vuông tại A. Tìm trực tâm H.

• A. Điểm A
• B. Điểm B
• C. Điểm C
• D. Không tồn tại

Đáp án: A. Điểm A Câu 2: Trong tam giác nhọn, nếu kẻ hai đường cao thì điểm nào là trực tâm?

• A. Điểm giao nhau
• B. Điểm giữa
• C. Điểm trên cạnh
• D. Điểm bên ngoài

Đáp án: A. Điểm giao nhau

6.2 Bài Tập Tự Luyện

• Tìm trực tâm của tam giác ABC với các đỉnh A(1, 3), B(4, 4), C(5, 1).
• Giải thích tại sao trực tâm của tam giác vuông lại trùng với đỉnh góc vuông.

Kết Luận

Kiến thức về trực tâm của tam giác là rất phong phú và hữu ích trong hình học. Hy vọng sau bài viết này, bạn đã có cái nhìn tổng quan và rõ nét về trực tâm, cách xác định và ứng dụng của nó. Hãy thực hành nhiều hơn với các bài tập để nắm vững kiến thức này nhé!