Cách chứng minh trực tâm trong tam giác hiệu quả

1. Giới Thiệu Về Trực Tâm Trong Tam Giác

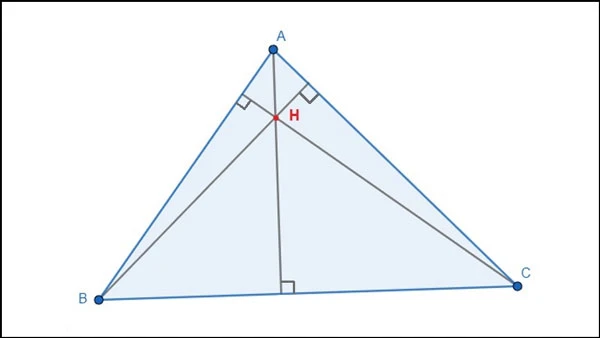
Trực tâm của tam giác là một khái niệm quan trọng trong hình học không gian, là điểm giao nhau của ba đường cao trong một tam giác. Việc hiểu và xác định vị trí của trực tâm không chỉ giúp nâng cao khả năng giải toán mà còn là nền tảng để xây dựng những kiến thức sâu hơn về hình học. Trong bài viết này, chúng tôi sẽ hướng dẫn chi tiết về cách chứng minh và tính chất của trực tâm trong tam giác.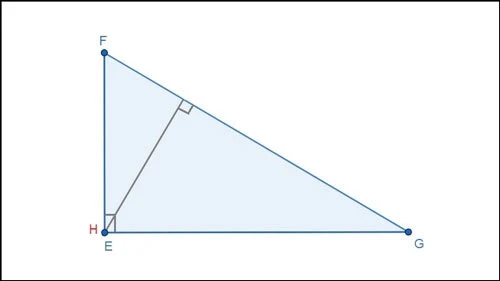

2. Khái Niệm Về Trực Tâm

2.1. Định Nghĩa Trực Tâm

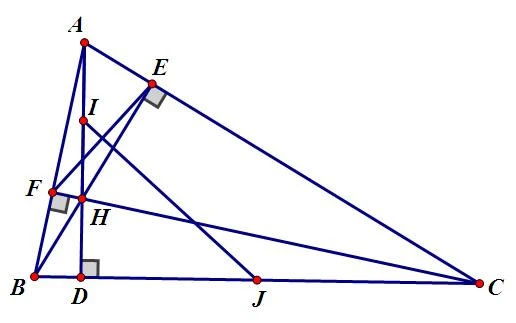
Trực tâm của một tam giác được xác định là điểm mà ba đường cao cắt nhau. Đường cao là đường thẳng vuông góc kẻ từ một đỉnh của tam giác đến đường thẳng chứa cạnh đối diện. Mỗi tam giác đều có ba đường cao và điểm giao nhau của chúng chính là trực tâm.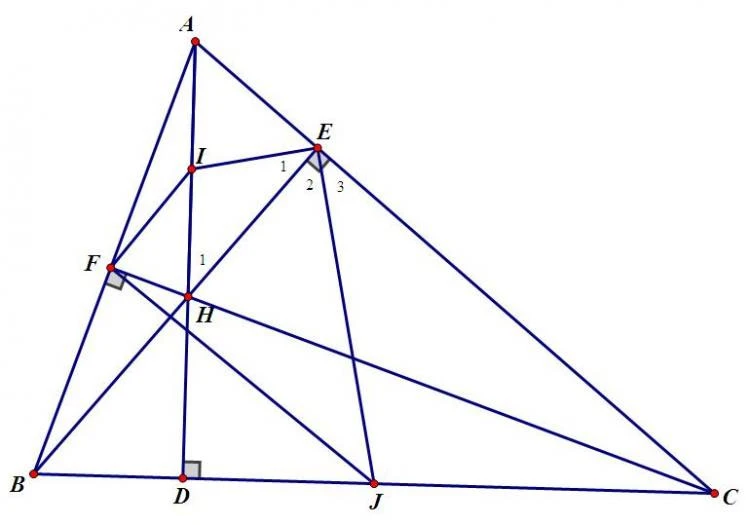

2.2. Các Loại Tam Giác Và Vị Trí Của Trực Tâm

• Tam giác nhọn: Trực tâm nằm trong tam giác.
• Tam giác vuông: Trực tâm trùng với đỉnh của góc vuông.
• Tam giác tù: Trực tâm nằm ngoài tam giác.

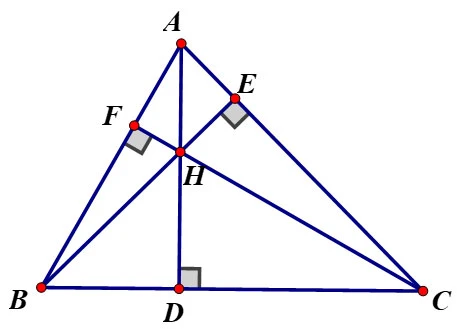
3. Tính Chất Của Trực Tâm

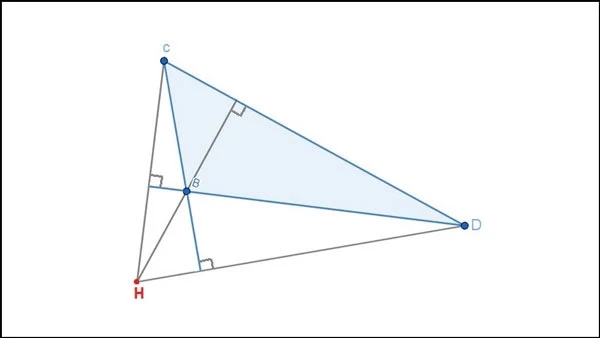
3.1. Tính Chất Cơ Bản

Trực tâm có nhiều tính chất đặc biệt, bao gồm:

• Tính chất 1: Trực tâm là điểm giao nhau của ba đường cao.
• Tính chất 2: Trực tâm cắt đường trung trực của hai cạnh tạo thành hai đoạn có độ dài bằng nhau.
• Tính chất 3: Trực tâm là tâm của đường tròn ngoại tiếp tam giác.
• Tính chất 4: Trực tâm của tam giác nhọn nằm bên trong, tam giác vuông nằm tại đỉnh góc vuông, và tam giác tù nằm ở bên ngoài.
• Tính chất 5: Trực tâm là điểm duy nhất trong tam giác mà tổng độ dài từ nó đến các đỉnh là nhỏ nhất.

4. Cách Xác Định Trực Tâm Trong Tam Giác

4.1. Xác Định Trực Tâm Trong Tam Giác Nhọn

• Kẻ hai đường cao từ hai đỉnh bất kỳ đến hai cạnh đối diện.
• Điểm giao nhau của hai đường cao chính là trực tâm và nằm bên trong tam giác.

4.2. Xác Định Trực Tâm Trong Tam Giác Vuông

• Trực tâm trùng với đỉnh góc vuông. Khi vẽ hai đường cao từ hai cạnh tạo thành góc vuông, chúng sẽ cắt nhau tại đỉnh của góc vuông.

4.3. Xác Định Trực Tâm Trong Tam Giác Tù

• Kẻ hai đường cao từ hai đỉnh của tam giác đối diện.
• Trực tâm sẽ nằm bên ngoài tam giác. Cần vẽ thêm một đường cao từ đỉnh góc tù xuống cạnh đối diện, điểm giao nhau của các đường cao đó chính là trực tâm.

5. Cách Chứng Minh Trực Tâm

Để chứng minh trực tâm trong tam giác, bạn có thể áp dụng một số phương pháp hình học cơ bản, chẳng hạn như:

5.1. Sử Dụng Tính Chất Đường Cao

• Chứng minh rằng ba đường cao cắt nhau tại một điểm duy nhất.
• Dùng định lý Pythagore để xác định các góc vuông.

5.2. Sử Dụng Định Lý Kahn

• Nếu ba vị trí của các đỉnh được xác định bằng các tọa độ, bạn có thể chứng minh rằng diện tích các tam giác được tạo ra bằng nhau.

6. Bài Tập Thực Hành Và Giải Đáp

6.1. Bài Tập Trắc Nghiệm

• Cho tam giác \( \Delta ABC \) vuông tại \( A \), hãy xác định trực tâm và cho biết lý do.
• Trong tam giác \( \Delta ABC \) có góc A rộng, hãy tìm vị trí của trực tâm và lý do.

6.2. Bài Tập Tự Luận

Bài 1: Giải thích tại sao trực tâm của tam giác vuông lại nằm tại đỉnh góc vuông. Giải: Vì hai cạnh tạo thành góc vuông cũng là các đường cao của tam giác vuông. Khi đó, điểm giao nhau của hai đường cao chính là trực tâm.

7. Kết Luận

Việc hiểu rõ về tính chất và cách chứng minh trực tâm trong tam giác là rất cần thiết cho việc giải các bài toán hình học nâng cao. Chúng tôi hy vọng rằng bài viết này sẽ giúp bạn nắm bắt nội dung hiệu quả và nâng cao khả năng tư duy toán học của mình. Hãy thường xuyên luyện tập và áp dụng các kiến thức đã học để phát triển kỹ năng giải toán của bạn!