Cách Chứng Minh Hình Thang Đơn Giản và Hiệu Quả

Hình thang là một trong những hình học cơ bản nhưng lại chứa đựng nhiều tính chất thú vị và các bài toán phong phú. Việc hiểu rõ hình thang, từ khái niệm đến cách chứng minh sẽ giúp ích rất nhiều trong học tập cũng như giải quyết các bài tập liên quan. Trong bài viết này, chúng ta sẽ cùng tìm hiểu các kiến thức cơ bản về hình thang và cách chứng minh hình thang một cách chi tiết.

I. Hình Thang

1. Khái Niệm về Hình Thang

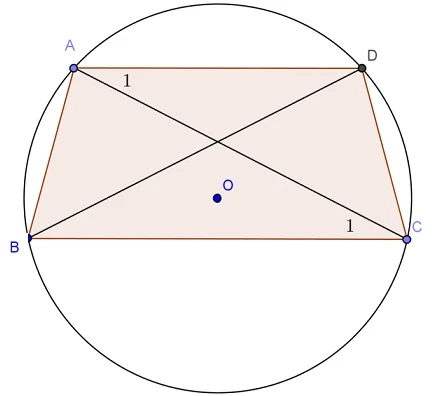
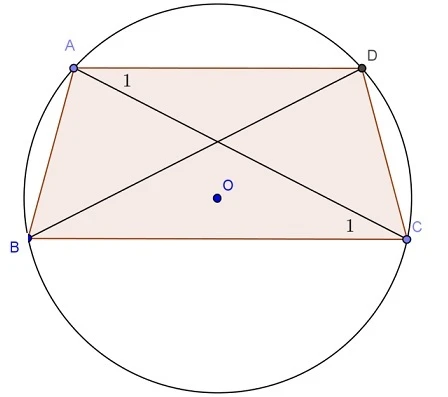
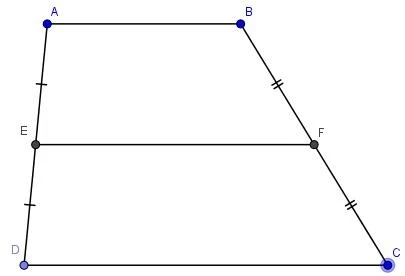
Hình thang là một loại tứ giác với đặc điểm nổi bật là có hai cạnh đối song song. Hai cạnh này gọi là hai "cạnh đáy" của hình thang.

Hình vẽ minh họa:

Giả sử ta có một hình thang ABCD với hai cạnh AB và CD là hai cạnh đáy, trong đó AB // CD.

2. Tính Chất Hình Thang

Hình thang có một số tính chất quan trọng mà chúng ta cần ghi nhớ:

- Tính Chất 1:

Hai góc kề một cạnh bên của hình thang có tổng bằng 180 độ.

• Ví dụ: Với hình thang ABCD (AB // CD):

- Góc A + Góc D = 180° - Góc B + Góc C = 180°

- Tính Chất 2:

Nếu hình thang có hai cạnh đáy bằng nhau, thì hai cạnh bên của nó cũng sẽ bằng nhau và song song.

• Ví dụ: Với hình thang ABCD (AB // CD) và AB = CD, sẽ dẫn đến AD = BC.

- Tính Chất 3:

Đường trung bình của hình thang là đoạn thẳng nối giữa hai trung điểm của hai cạnh bên và nó song song với hai cạnh đáy.

• Ví dụ: Gọi E là trung điểm của AD và F là trung điểm của BC, vậy đoạn thẳng EF sẽ là đường trung bình của hình thang ABCD.

3. Cách Chứng Minh Hình Thang

Để chứng minh một tứ giác là hình thang, có một số cách tiếp cận mà bạn có thể sử dụng:

- Cách 1: Chứng Minh Có Một Cặp Cạnh Đối Song Song

Giả sử ta có hình thang ABCD. Nếu chứng minh được có cặp cạnh AD // BC thì ABCD sẽ là hình thang.

- Cách 2: Chứng Minh Tổng Hai Góc Kề Một Cạnh Bên Bằng 180 Độ

Nếu tổng của hai góc kề một cạnh bên bằng 180 độ, thì tứ giác đó cũng là hình thang.

II. Hình Thang Cân

1. Khái Niệm Về Hình Thang Cân

Hình thang cân là trường hợp đặc biệt của hình thang, trong đó hai góc kề một cạnh đáy của hình thang bằng nhau.

2. Tính Chất Hình Thang Cân

- Tính Chất 1:

Trong hình thang cân, hai cạnh bên sẽ luôn bằng nhau.

- Tính Chất 2:

Hình thang cân có hai đường chéo bằng nhau.

- Tính Chất 3:

Hình thang cân luôn có thể nội tiếp một đường tròn.

3. Cách Chứng Minh Hình Thang Cân

Để chứng minh một hình thang là hình thang cân, có thể áp dụng các phương pháp sau:

- Cách 1: Hình Thang Có Hai Góc Kề Một Cạnh Đáy Bằng Nhau

Nếu hai góc kề đã cho bằng nhau, tức là bạn đã chứng minh rằng hình thang đó là hình thang cân.

- Cách 2: Hình Thang Có Hai Cạnh Bên Bằng Nhau

Nếu chứng minh được hai cạnh bên của hình thang bằng nhau, tứ giác cũng sẽ là hình thang cân.

- Cách 3: Hình Thang Có Hai Đường Chéo Bằng Nhau

Nếu chứng minh rằng hai đường chéo của hình thang bằng nhau, bạn cũng đã chứng minh được hình thang đó là hình thang cân.

Kết Luận

Hy vọng rằng, với những kiến thức trên, các bạn đã có cái nhìn tổng quát và rõ ràng hơn về hình thang và hình thang cân. Việc ghi nhớ các tính chất và cách chứng minh sẽ giúp bạn dễ dàng hơn trong việc giải quyết các bài toán liên quan. Hãy thực hành thường xuyên để củng cố kiến thức và đạt được kết quả cao trong học tập! Nếu bạn cần thêm thông tin hay hỗ trợ về kiến thức hình học, hãy tiếp tục theo dõi chúng tôi để không bỏ lỡ các bài học hữu ích tiếp theo. Việc nắm vững và áp dụng những kiến thức này sẽ mang đến cho bạn sự tự tin trong môn Toán.