Trọng tâm của tam giác: Chìa khóa để hiểu sâu sắc hình học
Trọng tâm tam giác không chỉ đơn giản là một điểm trong hình học mà còn mang đến cho chúng ta những kiến thức và ứng dụng phong phú trong nhiều lĩnh vực khác nhau. Từ văn hóa kiến trúc, nghệ thuật, cho đến khoa học kỹ thuật, trọng tâm tam giác đóng vai trò rất quan trọng. Bài viết này sẽ giúp bạn hiểu rõ hơn về trọng tâm của tam giác, từ định nghĩa, tính chất, phương pháp xác định cho đến những ứng dụng thực tiễn.
1. Trọng tâm tam giác là gì?
Trọng tâm của tam giác là điểm giao nhau của ba đường trung tuyến của tam giác đó. Đường trung tuyến là đường nối từ đỉnh của tam giác đến trung điểm của cạnh đối diện. Điểm này không chỉ mang ý nghĩa hình học mà còn được áp dụng trong nhiều lĩnh vực như vật lý, kỹ thuật và thiết kế.
1.1 Định nghĩa
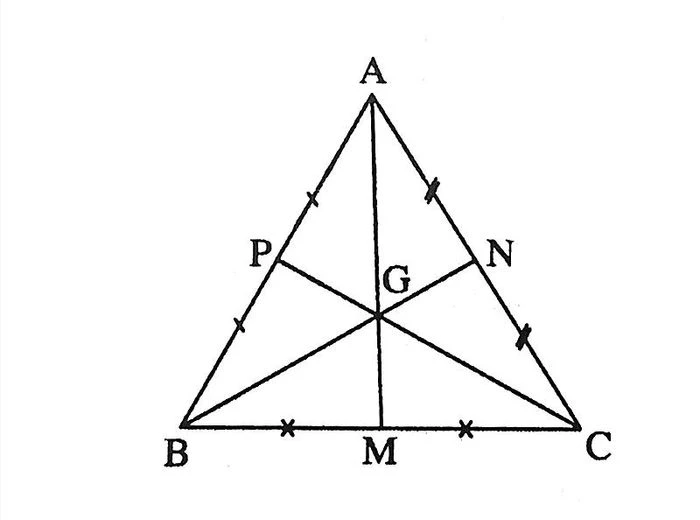
Theo sách giáo khoa hiện hành, trọng tâm G của tam giác ABC được định nghĩa như sau: “Trong một tam giác, ba đường trung tuyến cùng gặp nhau tại một điểm, gọi là trọng tâm”. Cụ thể:
- Tam giác ABC có ba đường trung tuyến: AM (từ A đến trung điểm M của cạnh BC), BN (từ B đến trung điểm N của cạnh AC), và CP (từ C đến trung điểm P của cạnh AB).
- Điểm G là trọng tâm của tam giác ABC, nơi ba đường trung tuyến giao nhau.
1.2 Ý nghĩa của trọng tâm
Trọng tâm được coi là "trung tâm quán tính" của tam giác, nơi mà nếu tái hiện bộ mặt một cách vô hình, tam giác sẽ cân bằng một cách hoàn hảo. Điều này được áp dụng trong thiết kế, kiến trúc và các ngành khoa học khác.
2. Những tính chất quan trọng của trọng tâm tam giác
Trọng tâm không chỉ là một điểm giao nhau đơn thuần mà còn sở hữu nhiều tính chất đặc biệt:

2.1 Tính chất phân chia
Trọng tâm tam giác chia mỗi đường trung tuyến thành hai đoạn, trong đó đoạn từ đỉnh đến trọng tâm dài gấp đôi đoạn còn lại. Cụ thể, với đường trung tuyến AM:
- AG: đoạn từ A đến G.
- GM: đoạn từ G đến M.
- Thì AG = 2 * GM.
2.2 Khoảng cách từ trọng tâm đến các đỉnh
Khoảng cách từ trọng tâm đến ba đỉnh của tam giác luôn bằng 2/3 chiều dài của từng đường trung tuyến cụ thể. Ví dụ:
- Nếu đường trung tuyến AM = 12 cm, thì AG = 8 cm và GM = 4 cm.
2.3 Trọng tâm và các hình tam giác đặc biệt
Trọng tâm của tam giác vuông, tam giác đều hay tam giác cân cũng có những tính chất đặc biệt mà ta cần lưu ý:
- Tam giác vuông: Trọng tâm nằm trên đường nối từ đỉnh đến trung điểm cạnh đối diện.
- Tam giác đều: Trọng tâm, trực tâm và tâm đường tròn nội tiếp cùng trùng tại một điểm.
- Tam giác cân: Trọng tâm đồng thời là đường cao, đường trung tuyến và đường phân giác.
3. Cách xác định trọng tâm tam giác
Để xác định trọng tâm của một tam giác, chúng ta có thể làm theo các bước sau:
3.1 Phương pháp vẽ
- Tìm trung điểm của hai cạnh bất kỳ. Ví dụ, tìm trung điểm M của cạnh BC.
- Nối đỉnh còn lại với trung điểm để tạo ra đường trung tuyến. Nối A với M.
- Làm tương tự với các cạnh còn lại.
- Điểm giao nhau của ba đường trung tuyến chính là trọng tâm G.
3.2 Sử dụng công thức tính toán
Nếu biết tọa độ của ba đỉnh A(x1, y1), B(x2, y2), C(x3, y3), ta có thể tính tọa độ của trọng tâm G bằng công thức:
\[ G = (\frac{x1 + x2 + x3}{3}, \frac{y1 + y2 + y3}{3}) \]
4. Ứng dụng của trọng tâm tam giác trong thực tế
Trọng tâm không chỉ có giá trị lý thuyết mà còn ứng dụng rộng rãi trong thực tế:
4.1 Trong thiết kế và xây dựng
Trọng tâm tam giác thường được sử dụng để cân bằng cấu trúc trong các công trình kiến trúc. Điều này đảm bảo rằng áp lực sẽ được phân bố đều, giúp tăng cường độ bền cho công trình.
4.2 Trong vật lý
Trong vật lý, trọng tâm cũng là cơ sở để tính toán quán tính và chuyển động của vật.
4.3 Trong nghệ thuật
Trong nghệ thuật, trọng tâm của hình tam giác được sử dụng để tạo ra sự cân bằng và tính thẩm mỹ cho các bức tranh, điêu khắc.
5. Bài tập thực hành về trọng tâm tam giác
Để củng cố kiến thức, dưới đây là một số bài tập mà bạn có thể thực hành:
5.1 Bài tập 1: Chứng minh tam giác cân
Cho tam giác ABC, trung tuyến BM = CN. BM cắt CN tại G. Chứng minh tam giác ABC cân tại A.
Lời giải: Vì BM và CN là hai đường trung tuyến, nên AG = 2/3 BM; AG = 2/3 CN. Khi đó, suy ra BN = CM và từ đó ta có AB = AC, chứng minh ABC là tam giác cân tại A.
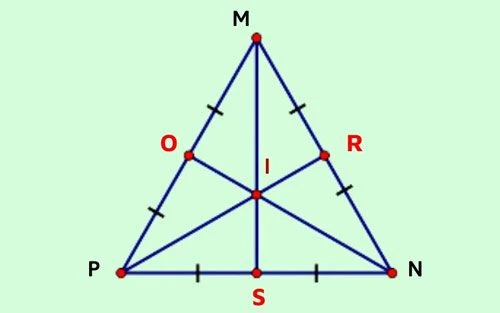
5.2 Bài tập 2: Trọng tâm tam giác đều
Cho I là trọng tâm của tam giác đều MNP. Chứng minh rằng IM = IN = IP.
Giải: Trong tam giác đều, các đoạn từ trọng tâm đến các đỉnh đều bằng nhau. Từ đó, suy ra IM = IN = IP.
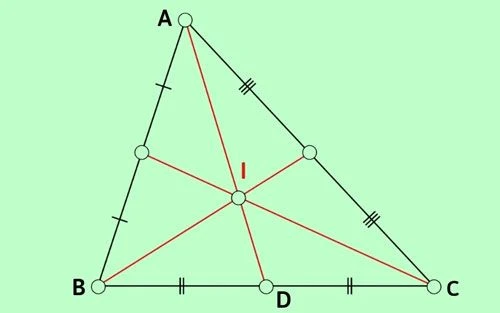
5.3 Bài tập 3: Tính chiều dài đoạn
Cho tam giác ABC có trung tuyến AD = 9cm và trọng tâm I. Hỏi độ dài của đoạn AI là bao nhiêu?
Lời giải: AI = (2/3) AD = (2/3) * 9 = 6 cm.
Kết luận
Trọng tâm của tam giác là một khái niệm quan trọng không thể thiếu trong học tập và ứng dụng thực tế. Hi vọng rằng bài viết này đã giúp bạn có cái nhìn tổng quan và sâu sắc hơn về trọng tâm tam giác, đồng thời củng cố thêm kiến thức để giải quyết các bài tập hình học một cách hiệu quả hơn. Hãy luôn nhớ rằng, nắm vững kiến thức không chỉ giúp bạn vượt qua bài kiểm tra mà còn áp dụng được trong nhiều lĩnh vực khác trong đời sống.