Khám Phá Thế Giới Ba Chiều
Trong cuộc sống hàng ngày, chúng ta thường xuyên gặp phải những khái niệm liên quan đến không gian ba chiều, từ những vật phẩm nhỏ nhất cho đến những công trình lớn lao. Một trong những yếu tố quan trọng khi nói đến các vật thể ba chiều chính là khả năng chứa đựng của chúng. Khả năng này không chỉ phản ánh kích thước của các vật thể mà còn ảnh hưởng đến nhiều lĩnh vực từ khoa học kỹ thuật cho đến nghệ thuật và thiết kế.
Định Nghĩa và Ý Nghĩa
Định Nghĩa Thể Tích
Cần bắt đầu bằng một định nghĩa đơn giản: thể tích là thước đo không gian mà một vật thể ba chiều chiếm giữ. Đơn vị tiêu chuẩn để đo thể tích trong hệ SI là mét khối (m³), mặc dù chúng ta cũng thường sử dụng các đơn vị khác như lít (l) hoặc gallon trong những bối cảnh cụ thể. Để xác định thể tích, chúng ta cần biết kích thước của vật thể thông qua các phép tính hình học cơ bản.
Ý Nghĩa trong Đời Sống
Việc hiểu thể tích không chỉ quan trọng trong toán học, mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực. Trong xây dựng, việc tính toán chính xác thể tích vật liệu là rất cần thiết để đảm bảo tính toàn vẹn cấu trúc. Trong khoa học, thể tích có thể ảnh hưởng đến các thí nghiệm hóa học và sinh học, trong đó sự chính xác của thể tích chất lỏng là yếu tố quyết định. Hơn nữa, trong ngành ẩm thực, thể tích giúp xác định lượng nguyên liệu cần thiết cho mỗi công thức nấu ăn.
Các Công Thức Tính Thể Tích
Thể Tích Của Các Hình Khối Cơ Bản
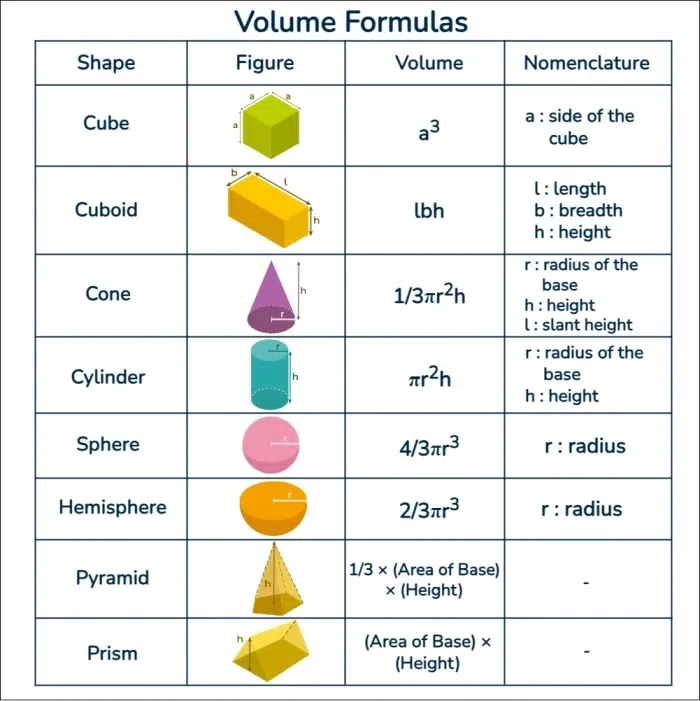
Để hiểu rõ hơn về cách tính thể tích, chúng ta hãy xem xét những hình khối phổ biến và công thức tương ứng của chúng.
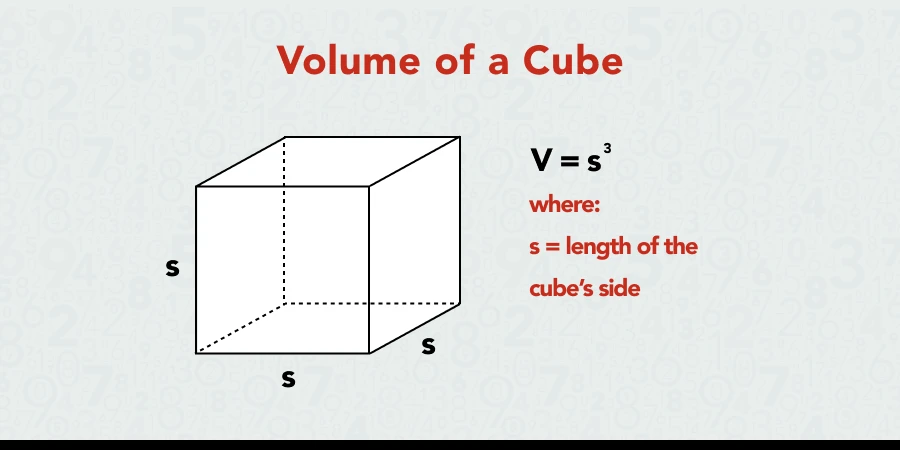
- Hình lập phương: Thể tích được tính bằng công thức V = a³, trong đó a là độ dài của một cạnh.
- Hình chữ nhật: Thể tích được tính bằng công thức V = l × w × h, với l là chiều dài, w là chiều rộng và h là chiều cao.
- Hình trụ: Thể tích được tính bằng công thức V = πr²h, trong đó r là bán kính đáy và h là chiều cao của hình trụ.
- Hình nón: Thể tích được tính theo công thức V = (1/3)πr²h.
- Hình cầu: Thể tích được tính bằng công thức V = (4/3)πr³.
Ví Dụ Cụ Thể
Giả sử bạn muốn tính thể tích của một hình trụ có bán kính 5 cm và chiều cao 10 cm. Bạn có thể áp dụng công thức trên như sau:
- Tính diện tích đáy: A = πr² = π (5)² = 25π cm².
- Tính thể tích: V = A × h = 25π × 10 = 250π cm³ ≈ 785 cm³.
Cách tính này có thể được áp dụng cho nhiều hình khối khác nhau, giúp dễ dàng xác định thể tích của chúng.
Ứng Dụng Thực Tiễn Của Thể Tích
Trong Khoa Học và Công Nghệ
Trong các lĩnh vực như hóa học và vật lý, thể tích đóng vai trò rất quan trọng. Chẳng hạn, trong thí nghiệm hóa học, việc đo đạc chính xác thể tích của dung dịch là rất cần thiết để đảm bảo kết quả chính xác. Hơn nữa, trong kỹ thuật, các kỹ sư sử dụng thể tích để tính toán dung tích của các bể chứa, ống dẫn hoặc các công trình khác.
Trong Kiến Trúc và Xây Dựng
Trong lĩnh vực xây dựng, việc tính toán thể tích là rất quan trọng. Các kiến trúc sư và kỹ sư xây dựng cần biết thể tích của các khối bê tông, thép hay gạch để đảm bảo rằng công trình sẽ đủ vững chãi và an toàn. Thực tế, nếu tính sai thể tích, có thể dẫn đến các vấn đề nghiêm trọng trong quá trình thi công.
Trong Thể Thao và Vận Động
Việc hiểu về thể tích cũng rất quan trọng trong thể thao. Ví dụ, trong bơi lội, thể tích cơ thể của một vận động viên có thể ảnh hưởng đến khả năng nổi và sức mạnh của họ trong nước. Hơn nữa, trong các môn thể thao như đua thuyền hay đua xe, thể tích của các phương tiện cũng cần được tính toán một cách chính xác để tối ưu hóa hiệu suất.
Kết Luận
Việc hiểu và áp dụng khái niệm về không gian ba chiều không chỉ giúp chúng ta có cái nhìn sâu sắc hơn về thế giới xung quanh mà còn góp phần vào nhiều lĩnh vực trong cuộc sống. Từ việc học hỏi và khám phá các hình khối, đến việc áp dụng các công thức trong thực tế, tất cả đều có ý nghĩa to lớn. Hy vọng rằng, qua bài viết này, bạn đã có thêm kiến thức về thể tích và những ứng dụng của nó trong cuộc sống hàng ngày.
Nếu bạn muốn tìm hiểu thêm về các khái niệm liên quan hoặc có bất cứ câu hỏi nào, đừng ngần ngại để lại ý kiến của bạn! Hãy cùng nhau khám phá thêm những điều thú vị về thế giới ba chiều xung quanh chúng ta.
