Hình học không gian là lĩnh vực thú vị của toán học, trong đó có những khái niệm được sử dụng rất nhiều trong thực tế. Một trong số đó là hình lăng trụ. Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu về định nghĩa, đặc điểm, các loại hình lăng trụ, công thức tính thể tích và những bài tập vận dụng liên quan đến hình lăng trụ.
1. Hình Lăng Trụ Là Gì?
Hình lăng trụ được định nghĩa là một loại đa giác có các mặt bên là hình bình hành và hai mặt đáy song song bằng nhau. Hình lăng trụ thường có nhiều ứng dụng trong các lĩnh vực như kiến trúc, kỹ thuật, và khoa học.

1.1. Hình Lăng Trụ Tam Giác Đều
Được biết đến như là một hình lăng trụ có mặt đáy là tam giác đều. Hình lăng trụ tam giác đều thường được ứng dụng trong việc tạo ra các cấu trúc vững chắc nhờ vào tính đối xứng tuyệt vời của hình tam giác.
1.2. Hình Lăng Trụ Tứ Giác Đều
Hình lăng trụ tứ giác đều có mặt đáy là hình tứ giác đều. Nó được ứng dụng rộng rãi trong việc thiết kế các công trình kiến trúc, đặc biệt là trong xây dựng các tòa nhà cao tầng.
2. Các Dạng Hình Lăng Trụ
Hình lăng trụ có nhiều dạng khác nhau tùy thuộc vào hình dạng của mặt đáy. Dưới đây là những dạng phổ biến của hình lăng trụ:
- Lăng Trụ Đứng: Là hình lăng trụ có cạnh bên vuông góc với mặt đáy. Chiều cao của hình lăng trụ là độ dài của cạnh bên. Mặt bên của hình lăng trụ đứng thường là hình chữ nhật.
- Lăng Trụ Đều: Là hình lăng trụ đứng có mặt đáy là đa giác đều. Mặt bên của lăng trụ đều cũng là các hình chữ nhật có kích thước bằng nhau.
- Hình Hộp: Là hình lăng trụ có đáy là hình bình hành, thường thấy trong các vật dụng hàng ngày như hộp quà hay hộp đựng đồ.
- Hình Hộp Đứng: Là hình lăng trụ đứng với đáy là hình bình hành.
- Hình Hộp Chữ Nhật: Là hình hộp đứng mà có đáy là hình chữ nhật.
- Hình Lập Phương: Khi hình lăng trụ đứng có đáy là hình vuông và các mặt bên cũng là hình vuông thì được gọi là hình lập phương.
3. Công Thức Tính Thể Tích Khối Lăng Trụ Đứng
Thể tích của khối lăng trụ đứng được tính bằng diện tích của mặt đáy nhân với chiều cao của hình lăng trụ:
Công thức tính thể tích
\[ V = B \cdot h \]
Trong đó:
- V: Thể tích khối lăng trụ (đơn vị m³)
- B: Diện tích mặt đáy (đơn vị m²)
- h: Chiều cao khối lăng trụ (đơn vị m)
4. Một Số Bài Tập Tính Thể Tích Khối Lăng Trụ Và Phương Pháp Giải
Bài Tập 1
Cho hình lăng trụ đứng ABC.A'B'C có đáy là tam giác đều cạnh a. Biết mặt phẳng (A'BC) tạo với đáy một góc 60°. Tìm thể tích khối lăng trụ.
Giải:
- Diện tích đáy của lăng trụ là:
\[ S_{ABC} = \frac{a^2 \sqrt{3}}{4} \]
- Thể tích khối lăng trụ là:
\[ V = S_{ABC} \cdot AA' = \frac{3a^3 \sqrt{3}}{8} \]
Bài Tập 2
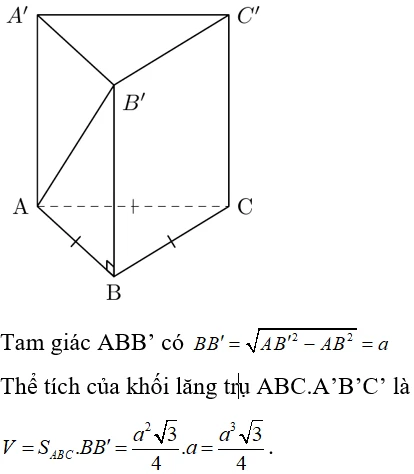
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Đường chéo của mặt bên ABB'A' là AB' = a√2. Tính thể tích của khối lăng trụ.
Giải:
- Thể tích khối lăng trụ là:
\[ V = S_{ABC} \cdot BB' = \frac{a^3 \sqrt{3}}{4} \]
Bài Tập 3
Cho lăng trụ xiên tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Hình chiếu của A' xuống (ABC) là tâm O đường tròn ngoại tiếp với tam giác ABC biết AA' hợp với đáy (ABC) một góc 60 độ.
Giải:
- Chứng minh rằng BB'C'C là hình chữ nhật.
- Tính thể tích khối lăng trụ.
Bài Tập 4
Cho hình hộp ABCD.A’B’C’D’ có đáy là hình chữ nhật với AB=√3, AD=√7. Hai mặt bên (ABB’A’) và (ADD’A’) tạo với đáy lần lượt các góc 45 độ và 60 độ. Tính thể tích khối hộp nếu biết cạnh bên bằng 1.
Giải:
- Tính toán dựa trên chiều cao và diện tích đáy để tìm ra thể tích chính xác.
Kết Luận
Bài viết này đã giúp bạn hiểu rõ hơn về hình lăng trụ, từ định nghĩa, các loại hinh đến công thức tính thể tích và bài tập thực tế. Hy vọng rằng kiến thức này sẽ hữu ích cho các bạn trong quá trình học tập và làm bài tập hình học không gian.
Nếu bạn có thắc mắc hay cần thêm thông tin gì về hình học không gian, hãy tham gia các khóa học hoặc tìm hiểu thêm tại Vuihoc.vn. Bên cạnh đó, đừng quên tham khảo những bài viết khác về công thức tính thể tích của các khối hình khác nhau để củng cố thêm kiến thức nhé!














