Giới thiệu về hình dạng ba đỉnh
Trong thế giới hình học, một trong những hình dạng đáng chú ý nhất là một khối hình phẳng có ba đỉnh và ba cạnh. Hình dạng này không chỉ đơn giản mà còn mang ý nghĩa sâu sắc trong nhiều lĩnh vực khác nhau, từ kiến trúc, nghệ thuật cho đến toán học.
Với ba điểm không thẳng hàng, hình dạng này tạo ra một cấu trúc vững chắc. Không chỉ có tính chất vật lý ổn định mà nó còn giúp cho việc nghiên cứu và ứng dụng trở nên thú vị hơn. Trong bài viết này, chúng ta sẽ khám phá sâu hơn về hình dạng này, từ định nghĩa, tính chất, đến phân loại và ứng dụng của nó trong đời sống.

Định nghĩa và tính chất cơ bản
Một hình dạng ba đỉnh là sự kết hợp của ba đoạn thẳng nối liền nhau, tạo thành một khối hình kín. Để có được hình dạng này, ba điểm phải không nằm trên cùng một đường thẳng. Giả sử chúng ta có ba điểm A, B và C, cấu trúc này sẽ được ký hiệu là ABC.
Các tính chất chính:
- Số cạnh và số đỉnh: Hình dạng ba đỉnh có ba cạnh và ba đỉnh.
- Góc: Tổng của các góc trong một hình này luôn bằng 180 độ. Mỗi góc có thể thay đổi tùy thuộc vào loại hình: góc nhọn, góc vuông, hoặc góc tù.
- Diện tích: Diện tích của hình dạng này có thể được tính bằng nhiều công thức khác nhau, tùy thuộc vào thông tin mà chúng ta có.
Phân loại hình dạng ba đỉnh
Hình dạng này có thể được phân loại dựa trên độ dài của các cạnh và các góc của nó. Việc phân loại này không chỉ giúp trong việc nhận diện mà còn tạo điều kiện cho việc áp dụng các công thức tính toán phù hợp.
1. Phân loại theo độ dài cạnh:
- Hình đều: Tất cả ba cạnh có độ dài bằng nhau. Các góc cũng sẽ bằng nhau, thường là 60 độ.
- Hình cân: Hai cạnh có độ dài bằng nhau. Các góc đối diện với hai cạnh bằng nhau.
- Hình thường: Tất cả các cạnh có độ dài khác nhau.
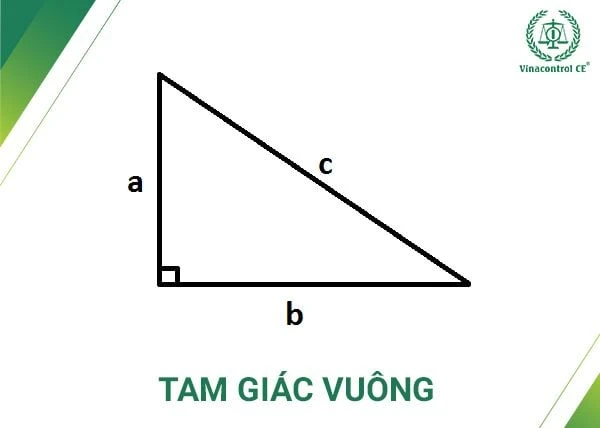
2. Phân loại theo góc:
- Hình nhọn: Tất cả các góc đều nhỏ hơn 90 độ.
- Hình vuông: Một góc bằng 90 độ. Đây là loại hình rất phổ biến trong kiến trúc.
- Hình tù: Một góc lớn hơn 90 độ.
Ứng dụng trong đời sống
Hình dạng ba đỉnh không chỉ là một khái niệm trừu tượng trong toán học, mà còn có ứng dụng rất thực tiễn trong nhiều lĩnh vực khác nhau.
1. Kiến trúc và xây dựng
Hình dạng này thường được sử dụng trong thiết kế các công trình kiến trúc. Nhờ vào tính ổn định của nó, nhiều công trình đã được xây dựng theo hình dạng này để đảm bảo an toàn và sự chắc chắn.
2. Nghệ thuật
Trong nghệ thuật, hình dạng này thường được các nghệ sĩ sử dụng để tạo ra các tác phẩm độc đáo và sáng tạo. Bằng cách kết hợp các hình dạng này, họ có thể tạo ra nhiều tác phẩm nghệ thuật phong phú và đa dạng.
3. Toán học và vật lý
Trong toán học, hình dạng này là cơ sở để phát triển nhiều khái niệm khác nhau, từ hình học đến đại số. Nó cũng là một phần quan trọng của nhiều lý thuyết vật lý, giúp giải thích các hiện tượng tự nhiên.
4. Công nghệ
Nhiều thiết bị và công nghệ hiện đại sử dụng hình dạng này trong thiết kế, từ các thiết bị điện tử, ô tô đến máy bay. Hình dạng này giúp giảm trọng lượng và tăng hiệu suất.
Công thức tính diện tích
Để tính diện tích của hình dạng ba đỉnh, có nhiều công thức khác nhau tùy thuộc vào thông tin có sẵn.
1. Công thức cơ bản
Diện tích của hình này có thể được tính bằng công thức:
\[ S = \frac{a \times h}{2} \]
Trong đó:
- \( S \) là diện tích.
- \( a \) là độ dài của đáy.
- \( h \) là chiều cao từ đỉnh đến đáy.
2. Công thức Heron
Nếu biết độ dài của tất cả ba cạnh, diện tích có thể được tính bằng công thức Heron:
\[ S = \sqrt{s(s-a)(s-b)(s-c)} \]
Trong đó:
- \( s = \frac{a+b+c}{2} \) là nửa chu vi.
- \( a, b, c \) lần lượt là độ dài của ba cạnh.

Kết luận
Hình dạng ba đỉnh là một phần không thể thiếu trong thế giới hình học. Từ các tính chất cơ bản đến ứng dụng trong đời sống, hình dạng này đã chứng minh được vai trò quan trọng của mình trong nhiều lĩnh vực khác nhau. Việc hiểu rõ về nó không chỉ giúp nâng cao kiến thức về hình học mà còn mở ra nhiều cơ hội ứng dụng trong thực tiễn.
Từ việc thiết kế công trình kiến trúc cho đến việc tạo ra các tác phẩm nghệ thuật độc đáo, hình dạng này chắc chắn sẽ tiếp tục tồn tại và phát triển trong tương lai.

















