
Tính Thể Tích Khối Trụ: Một Hướng Dẫn Chi Tiết

1. Khối Trụ Tròn Xoay Là Gì?
Khối trụ tròn xoay là một khái niệm cơ bản trong hình học, được định nghĩa là hình thể tạo ra khi xoay một hình phẳng quanh một trục cố định. Hình trụ này chiếm một không gian nhất định trong không gian ba chiều. Dưới đây là những điểm chính về khối trụ tròn xoay:
- Đáy Hình Tròn: Khối trụ có hai mặt đáy hình tròn, với diện tích đáy được tính bằng công thức \(A = \pi r^2\) (trong đó \(r\) là bán kính của đáy tròn).
- Trục Xoay: Là đường thẳng đi qua tâm hai mặt đáy, quyết định hình dạng của khối trụ.
- Chiều Cao: Khoảng cách giữa hai mặt đáy của khối trụ.
- Mặt Bên Cong: Là bề mặt tạo thành khi hai đáy quay quanh trục, tạo ra hình dạng liên tục.
2. Tính Thể Tích Khối Trụ Tròn Xoay
Thể tích của khối trụ tròn xoay được tính bằng công thức sau:
\[
V = A \cdot h = \pi r^2 \cdot h
\]
2.1 Giải Thích Công Thức
- \(V\): Thể tích khối trụ
- \(A\): Diện tích đáy của khối trụ
- \(h\): Chiều cao của khối trụ
- \(r\): Bán kính của đáy tròn
- \(\pi\): Hằng số khoảng 3.14159
Công thức trên hoàn toàn đơn giản và dễ áp dụng, cho phép bạn tính toán thể tích của bất kỳ khối trụ nào chỉ cần bạn biết bán kính và chiều cao.
3. Ứng Dụng Thực Tế
Khối trụ tròn xoay không chỉ tồn tại trong sách vở hay trong phòng học, mà còn xuất hiện khắp nơi trong cuộc sống. Dưới đây là một số ứng dụng tiêu biểu:
- Thiết kế kiến trúc: Các cột trụ trong các công trình xây dựng thường là hình trụ.
- Sản xuất công nghiệp: Nhiều sản phẩm như chai nước, ống nước, v.v... cũng có hình dạng khối trụ.
- Khoa học và công nghệ: Ứng dụng trong vật liệu, chất lỏng và trong nhiều lĩnh vực khoa học khác.

4. Ví Dụ Minh Hoạ
Dưới đây là một số bài tập ví dụ để giúp bạn hiểu rõ hơn về cách tính thể tích khối trụ tròn xoay.
4.1 Ví dụ 1
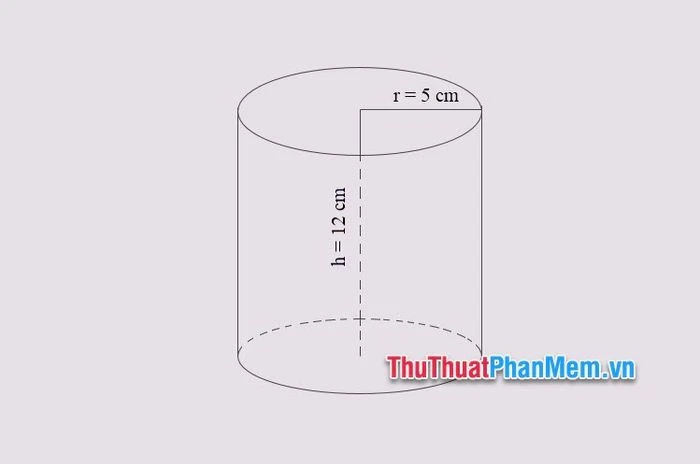
Đề bài: Một khối trụ tròn xoay có bán kính đáy \(r = 4 cm\) và chiều cao \(h = 10 cm\). Tính thể tích của khối trụ này.
Lời giải: Áp dụng công thức tính thể tích:
\[
V = \pi r^2 h = \pi \cdot 4^2 \cdot 10 = \pi \cdot 16 \cdot 10 = 160\pi \approx 502.65 \, cm^3
\]
4.2 Ví dụ 2
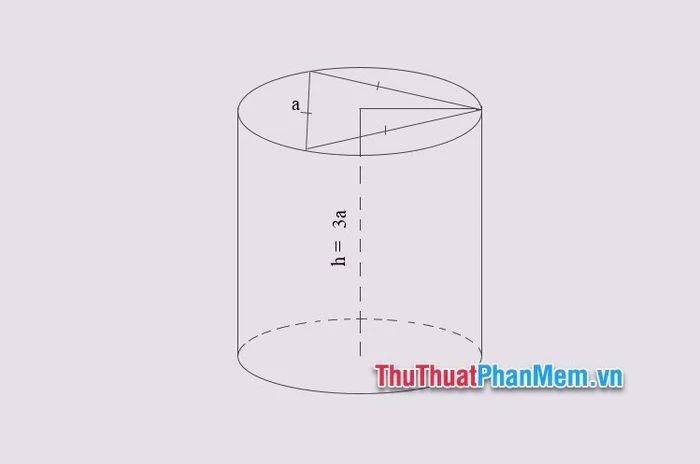
Đề bài: Một khối trụ tròn xoay có đáy là hình tròn ngoại tiếp của một tam giác đều cạnh \(a\), biết chiều cao của khối trụ là \(2a\). Tính thể tích khối trụ tròn xoay.
Lời giải: Bán kính của hình tròn ngoại tiếp tính bằng công thức:
\[
R = \frac{a}{\sqrt{3}}
\]
Áp dụng công thức tính thể tích:
\[
V = \pi R^2 h = \pi \left(\frac{a}{\sqrt{3}}\right)^2 \cdot 2a = \pi \cdot \frac{a^2}{3} \cdot 2a = \frac{2\pi a^3}{3}
\]
5. Những Lưu Ý Khi Tính Thể Tích Khối Trụ
- Kiểm tra đơn vị: Đảm bảo bán kính và chiều cao có cùng đơn vị trước khi tính thể tích.
- Cẩn thận với số liệu: Sai sót trong việc xác định bán kính hoặc chiều cao có thể dẫn đến sai kết quả thể tích.
6. Tóm Lại
Cách tính thể tích khối trụ tròn xoay là một kỹ năng quan trọng trong học tập và nghiên cứu. Nắm vững công thức có thể giúp bạn áp dụng chúng vào nhiều lĩnh vực khác nhau trong cuộc sống hàng ngày. Với những kiến thức đã trình bày, hy vọng bạn sẽ thành công trong việc tính toán và áp dụng thể tích khối trụ tròn xoay một cách hiệu quả nhất.

















