Hiểu Rõ Về Tính Toán Số Tiền Lãi Trong Ngân Hàng
Trong thế giới tài chính ngày nay, việc tính toán số tiền lãi khi gửi tiết kiệm hay vay vốn ngân hàng là rất quan trọng. Điều này không chỉ giúp bạn có được cái nhìn tổng quát về tài chính cá nhân mà còn hỗ trợ bạn trong việc lập kế hoạch chi tiêu và đầu tư hợp lý. Bài viết này sẽ đi sâu vào các khía cạnh khác nhau của việc tính toán lãi suất, từ lý thuyết cơ bản đến các công thức cụ thể, giúp bạn dễ dàng áp dụng trong thực tế.
Lãi Suất Là Gì?
Lãi suất là tỷ lệ phần trăm mà ngân hàng (hoặc tổ chức tài chính) tính cho số tiền bạn gửi hoặc vay. Nó có thể được xem như là "chi phí" để sử dụng tiền của người khác (trong trường hợp vay) hoặc là "phần thưởng" cho việc bạn gửi tiền vào ngân hàng (trong trường hợp tiết kiệm).
Có hai loại lãi suất chính:
- Lãi suất đơn: Đây là lãi suất được tính chỉ trên số tiền gốc ban đầu mà bạn gửi hoặc vay.
- Lãi suất kép: Đây là lãi suất được tính trên cả số tiền gốc và số tiền lãi đã tích lũy từ trước.
Việc hiểu rõ về lãi suất sẽ giúp bạn có những quyết định tài chính thông minh hơn.
Công Thức Tính Lãi Suất
Để tính được số tiền lãi bạn sẽ nhận được từ ngân hàng hoặc số tiền bạn phải trả khi vay, bạn cần nắm rõ công thức tính lãi suất. Dưới đây là công thức cơ bản cho từng loại lãi suất:
1. Tính Lãi Suất Đơn
Công thức tính lãi suất đơn được thể hiện như sau:
\[ \text{Lãi} = \text{Số tiền gốc} \times \text{Lãi suất} \times \text{Thời gian} \]
Trong đó:
- Số tiền gốc: Số tiền bạn gửi hoặc vay.
- Lãi suất: Tỷ lệ lãi suất tính theo phần trăm.
- Thời gian: Thời gian tính lãi (thường tính bằng năm).
2. Tính Lãi Suất Kép
Công thức tính lãi suất kép phức tạp hơn một chút:
\[ A = P \times (1 + r/n)^{nt} \]
Trong đó:
- A: Tổng số tiền sau thời gian t.
- P: Số tiền gốc ban đầu.
- r: Lãi suất hàng năm (tính theo phần trăm).
- n: Số lần lãi được tính trong một năm.
- t: Số năm gửi hoặc vay.
Việc sử dụng công thức lãi suất kép giúp bạn nhận ra rằng, theo thời gian, số tiền lãi sẽ ngày càng nhiều hơn do lãi đã sinh lãi.
Ứng Dụng Thực Tế Của Tính Toán Lãi Suất
Tính toán lãi suất không chỉ là lý thuyết mà còn có ứng dụng thực tế rất cao trong cuộc sống hàng ngày. Dưới đây là một số tình huống cụ thể mà bạn có thể áp dụng kiến thức này:
1. Gửi Tiết Kiệm Ngân Hàng
Khi bạn gửi tiền vào ngân hàng, việc tính toán số tiền lãi bạn sẽ nhận được sau một thời gian là rất quan trọng. Giả sử bạn gửi 10 triệu đồng với lãi suất 5% một năm trong thời gian 2 năm, bạn có thể tính số tiền lãi như sau:
\[ Lãi = 10,000,000 \times 0.05 \times 2 = 1,000,000 \text{ đồng} \]
- Lãi suất kép (nếu lãi được tính hàng năm):
\[ A = 10,000,000 \times (1 + 0.05)^{2} = 10,000,000 \times 1.1025 \approx 11,025,000 \text{ đồng} \]
Như vậy, bạn sẽ nhận được khoảng 1,025,000 đồng lãi nếu tính theo lãi suất kép.
2. Vay Ngân Hàng
Khi bạn cần vay tiền, việc hiểu rõ về cách tính lãi suất sẽ giúp bạn có kế hoạch trả nợ hợp lý. Giả sử bạn vay 50 triệu đồng với lãi suất 7% một năm trong thời gian 3 năm, bạn có thể tính số tiền lãi như sau:
\[ Lãi = 50,000,000 \times 0.07 \times 3 = 10,500,000 \text{ đồng} \]
- Lãi suất kép (nếu lãi được tính hàng năm):
\[ A = 50,000,000 \times (1 + 0.07)^{3} = 50,000,000 \times 1.225043 = 61,252,150 \text{ đồng} \]
Điều này có nghĩa là bạn sẽ phải trả tổng cộng khoảng 61,252,150 đồng sau 3 năm nếu tính theo lãi suất kép.
Kết Luận
Việc nắm rõ cách tính toán số tiền lãi trong ngân hàng không chỉ giúp bạn quản lý tài chính cá nhân một cách hiệu quả mà còn đóng góp cho việc ra quyết định đầu tư hoặc chi tiêu. Hiểu được các khái niệm và công thức liên quan đến lãi suất là một phần quan trọng trong việc xây dựng nền tảng tài chính vững chắc.
Hãy nhớ rằng, dù bạn đang gửi tiền tiết kiệm hay vay vốn, việc lựa chọn loại lãi suất phù hợp và tính toán chính xác sẽ giúp bạn tối ưu hóa lợi ích tài chính của mình. Hy vọng rằng bài viết này đã mang đến cho bạn cái nhìn tổng quan và hữu ích về vấn đề này.
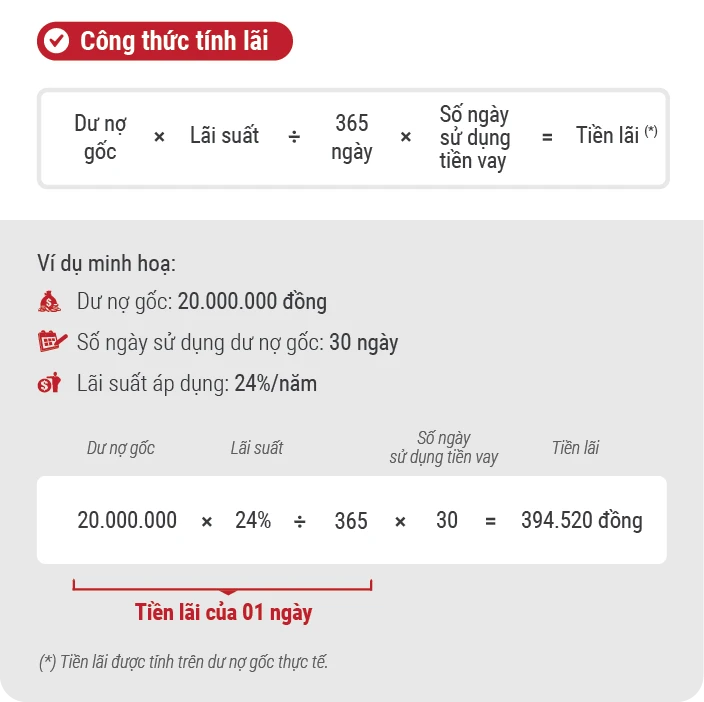
Hãy luôn theo dõi và cập nhật thông tin về lãi suất từ các ngân hàng để có thể đưa ra quyết định tốt nhất cho tài chính của bạn!
