Tính Diện Tích Tam Giác Cân: Một Khái Niệm Cơ Bản Trong Hình Học
Hình tam giác là một trong những hình học đơn giản nhưng cũng vô cùng thú vị. Trong đó, tam giác cân là một loại tam giác có những đặc điểm riêng biệt mà chắc chắn bạn sẽ muốn tìm hiểu. Một trong những vấn đề thường gặp liên quan đến tam giác cân chính là cách tính diện tích của nó. Hãy cùng khám phá mọi điều về "tính diện tích tam giác cân" qua bài viết này.
Công Thức Tính Diện Tích Tam Giác
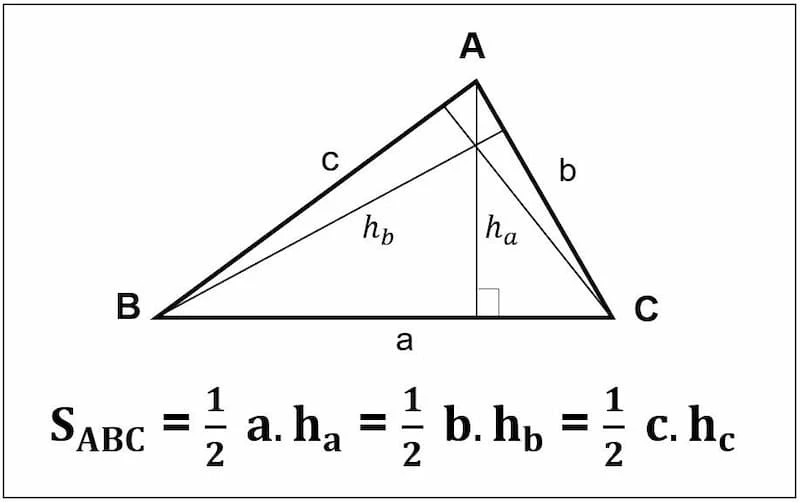
Để bắt đầu, công thức tính diện tích của một hình tam giác nói chung là:
S = (a x h) / 2
Trong đó:
- S là diện tích tam giác.
- a là độ dài đáy của tam giác.
- h là chiều cao từ đỉnh vuông góc xuống đáy.
Ví Dụ Cụ Thể
Giả sử bạn có một tam giác với độ dài đáy là 5m và chiều cao là 24dm.
- Chiều cao 24dm bằng 2.4m.
- Áp dụng công thức, chúng ta có:
\[
S = (5 x 2.4) / 2 = 6m^2
\]
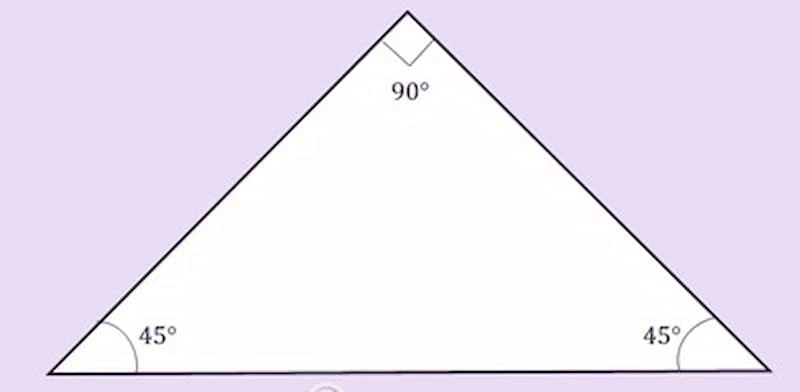
Các Loại Tam Giác
Tam giác có thể được phân loại theo nhiều cách khác nhau, dựa trên các đặc điểm của các cạnh và góc. Sau đây là 7 loại tam giác phổ biến:
- Tam giác vuông: Có một góc bằng 90 độ.
- Tam giác cân: Có hai cạnh bằng nhau.
- Tam giác đều: Cả ba cạnh đều bằng nhau.
- Tam giác nhọn: Tất cả ba góc nhỏ hơn 90 độ.
- Tam giác tù: Có một góc lớn hơn 90 độ.
- Tam giác thường: Không có cạnh và góc nào bằng nhau.
- Tam giác vuông cân: Vừa vuông vừa cân.
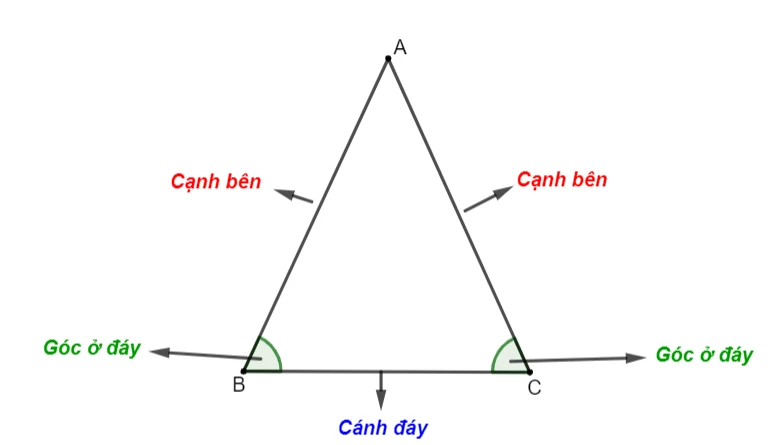
Cách Tính Diện Tích Tam Giác Cân
Đối với tam giác cân, công thức tính diện tích vẫn theo quy tắc cơ bản, nhưng có một điều thú vị là chiều cao sẽ thấy dễ dàng hơn để tìm ra.
Công Thức Chi Tiết
S = (a x h) / 2
- a là độ dài cạnh đáy.
- h là chiều cao.
Ví Dụ Tính Toán
- Ví dụ 1: Tính diện tích tam giác cân với độ dài cạnh đáy bằng 6cm và chiều cao bằng 7cm.
\[
S = (6 x 7) / 2 = 21 cm^2
\]
- Ví dụ 2: Tam giác cân với độ dài cạnh đáy bằng 5m và chiều cao 3.2m.
\[
S = (5 x 3.2) / 2 = 8 m^2
\]
Các Công Thức Tính Diện Tích Khác
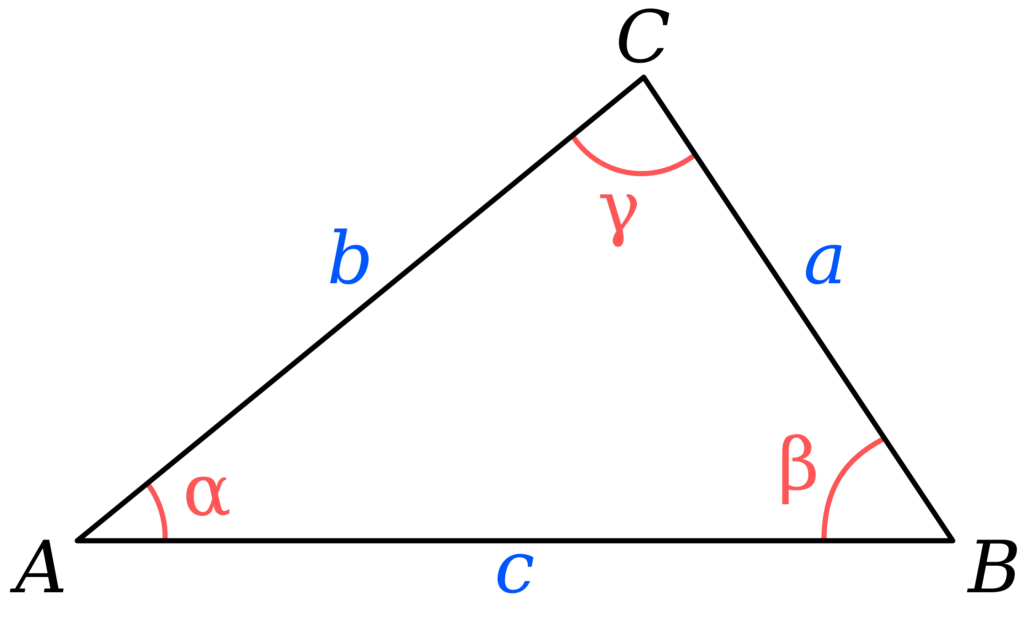
Trên thực tế, có nhiều loại tam giác, mỗi loại cần có các công thức tương ứng để tính diện tích:
Diện Tích Tam Giác Đều
S = (a x h) / 2 (tương tự như tam giác cân).
Diện Tích Tam Giác Vuông
Công thức tính diện tích tam giác vuông sẽ là:
S = (a x b) / 2
Trong đó a và b là độ dài của hai cạnh góc vuông.
Công Thức Tính Diện Tích Tam Giác Trong Không Gian
Khi chuyển sang không gian Oxyz, việc tính diện tích tam giác trở nên phức tạp hơn. Tuy nhiên, chúng ta có thể sử dụng tích có hướng để tính toán diện tích.
Kiến Thức Cần Nhớ
Để học tốt cách tính diện tích tam giác, các bạn cần nắm rõ một số khái niệm căn bản như:
- Khái niệm về hình tam giác: Hình tam giác có ba đỉnh không thẳng hàng và ba cạnh nối các đỉnh này.
- Tính chất cơ bản: Tổng ba góc luôn bằng 180 độ, và tổng chiều dài hai cạnh luôn lớn hơn chiều dài cạnh còn lại.
Một Số Dạng Bài Tập Cơ Bản & Nâng Cao
- Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao.
- Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao.
- Dạng 3: Tính chiều cao khi biết diện tích và đáy.
Bí Quyết Ghi Nhớ Công Thức Tính Diện Tích Hình Tam Giác
- Nắm vững kiến thức cơ bản: Theo dõi và kiểm tra thường xuyên giúp củng cố kiến thức.
- Thực hành thường xuyên: Cùng con làm các bài tập khác nhau để nâng cao khả năng.
Ứng Dụng Trong Thực Tiễn
Công thức diện tích tam giác không chỉ có ý nghĩa trong lý thuyết mà còn áp dụng rộng rãi trong thực tế, những lĩnh vực như:
- Xây dựng: Tính diện tích mái nhà, tường và các cấu trúc.
- Vật lý: Tính toán diện tích bề mặt các vật thể hình tam giác.
- Kiến trúc: Thiết kế công trình có hình dạng tam giác.
Kết Luận
Hy vọng qua bài viết này, bạn đã có cái nhìn tổng quan về cách tính diện tích tam giác cân và hiểu rõ hơn về các loại hình tam giác. Nắm vững công thức và áp dụng thực hành thường xuyên sẽ giúp cải thiện đáng kể kỹ năng giải toán của bạn. Hãy cùng nhau học tập hiệu quả và thú vị hơn nhé!



















