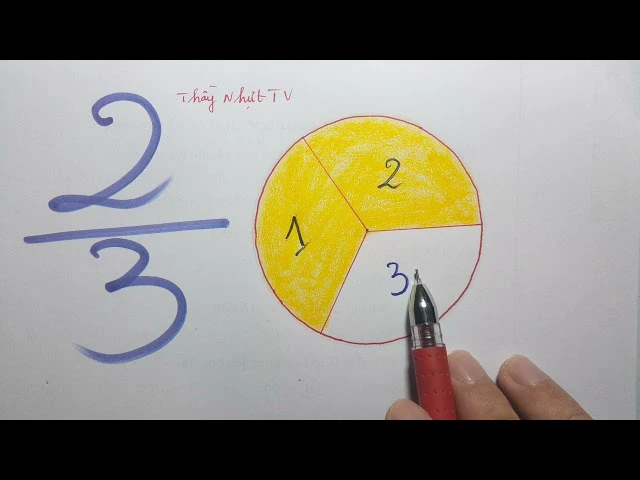Giới thiệu về tỷ lệ phần
Trong toán học, việc làm quen với các tỷ lệ phần là một phần quan trọng trong việc hiểu biết về phân số, tỷ lệ, và các phép tính cơ bản. Một trong những tỷ lệ phần phổ biến mà chúng ta thường gặp trong cuộc sống hàng ngày là tỷ lệ 2 phần 3. Tỷ lệ này không chỉ có giá trị trong toán học mà còn có ứng dụng thực tế trong nhiều lĩnh vực như nấu ăn, đo lường và tài chính. Bài viết này sẽ giúp bạn hiểu rõ hơn về tỷ lệ này, cách chuyển đổi nó sang phần trăm, và ứng dụng của nó trong đời sống.
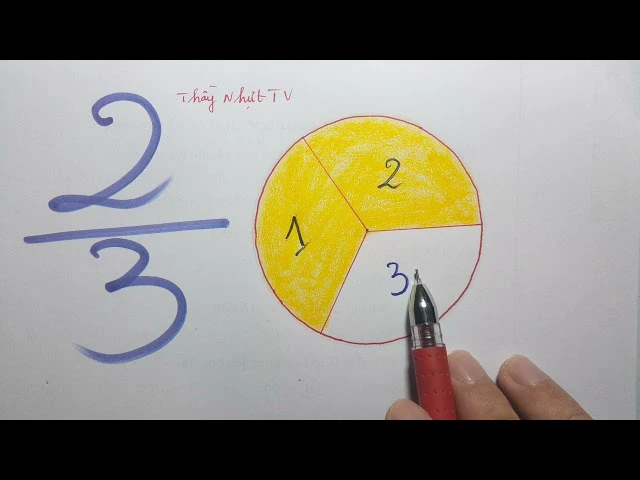
Tìm hiểu về tỷ lệ 2 phần 3
Để hiểu rõ về tỷ lệ 2 phần 3, trước hết, chúng ta cần nắm vững khái niệm về phân số. Phân số được cấu thành từ hai phần, phần tử (tử số) và mẫu số. Trong đó, tử số biểu thị số lượng phần mà chúng ta có, còn mẫu số biểu thị tổng số phần mà một đơn vị được chia thành.
Cách tính toán tỷ lệ phần
Khi nói đến 2 phần 3, điều này có nghĩa là chúng ta đang xét đến 2 phần trong tổng số 3 phần. Để tính toán giá trị cụ thể của tỷ lệ này, bạn có thể thực hiện phép tính:
\[
\frac{2}{3} \approx 0.6667
\]
Kết quả này có thể được diễn đạt dưới dạng phần trăm bằng cách nhân với 100:
\[
0.6667 \times 100 \approx 66.67\%
\]
Vậy 2 phần 3 tương đương với khoảng 66.67%. Điều này có thể được áp dụng trong nhiều ngữ cảnh khác nhau, từ việc chia sẻ thức ăn cho đến đánh giá kết quả học tập.

Cách chuyển đổi tỷ lệ phần sang phần trăm
Chuyển đổi từ tỷ lệ phần sang phần trăm là một kỹ năng hữu ích trong nhiều tình huống. Để thực hiện phép chuyển đổi này, bạn chỉ cần làm theo các bước sau:
- Xác định tỷ lệ phần: Như đã đề cập, tỷ lệ 2 phần 3 có thể viết dưới dạng phân số là \(\frac{2}{3}\).
- Tính giá trị thập phân: Chia tử số cho mẫu số. Với tỷ lệ này, bạn sẽ nhận được 0.6667.
- Chuyển đổi sang phần trăm: Nhân giá trị thập phân với 100. Kết quả sẽ là 66.67%.
Ví dụ thực tế
Giả sử bạn có một giỏ trái cây và bạn muốn biết số lượng trái cây mà bạn đã chia sẻ so với tổng số trái cây có trong giỏ. Nếu bạn có 3 quả táo và bạn đã chia sẻ 2 quả, bạn có thể tính toán như sau:
- Số lượng đã chia sẻ: 2
- Tổng số quả táo: 3
Tỷ lệ quả táo đã chia sẻ là:
\[
\frac{2}{3} \approx 66.67\%
\]
Điều này có nghĩa là bạn đã chia sẻ 66.67% số táo trong giỏ.
Ứng dụng trong đời sống hàng ngày
Tỷ lệ 2 phần 3 có nhiều ứng dụng trong cuộc sống hàng ngày, từ các lĩnh vực như nấu ăn, phân chia tài sản đến các bài kiểm tra trong giáo dục.
Nấu ăn
Trong nấu ăn, việc sử dụng tỷ lệ phần là rất quan trọng. Ví dụ, nếu bạn muốn làm một công thức cần 3 cốc bột và bạn chỉ muốn làm 2/3 công thức, bạn sẽ cần tính toán lại lượng bột cần thiết. Áp dụng tỷ lệ 2 phần 3 vào công thức, bạn sẽ nhận được:
\[
\text{Lượng bột cần thiết} = \frac{2}{3} \times 3 \text{ cốc} = 2 \text{ cốc}
\]
Phân chia tài sản
Trong lĩnh vực tài chính, khi chia tài sản giữa các thành viên trong gia đình, tỷ lệ 2 phần 3 cũng có thể được ứng dụng. Ví dụ, nếu một tài sản có tổng giá trị 300 triệu đồng và bạn muốn chia cho 3 người, người có 2 phần sẽ nhận được:
\[
\text{Giá trị nhận được} = \frac{2}{3} \times 300 \text{ triệu} = 200 \text{ triệu}
\]
Giáo dục
Trong giáo dục, các bài kiểm tra thường được chấm điểm theo tỷ lệ phần. Nếu bạn đạt 2/3 số câu hỏi đúng trong một bài kiểm tra 30 câu hỏi, bạn sẽ có:
\[
\text{Số câu hỏi đúng} = \frac{2}{3} \times 30 = 20 \text{ câu}
\]
Điều này có thể giúp bạn xác định được khả năng của mình trong môn học đó và so sánh với các bạn khác.
Kết luận
Tỷ lệ 2 phần 3 không chỉ đơn thuần là một khái niệm toán học mà còn mang lại nhiều giá trị thực tiễn trong cuộc sống hàng ngày. Từ việc nấu ăn cho đến phân chia tài sản và đánh giá kết quả học tập, việc hiểu rõ về tỷ lệ này giúp chúng ta áp dụng một cách hiệu quả. Việc chuyển đổi tỷ lệ phần thành phần trăm cũng là một kỹ năng cần thiết cho nhiều người, đặc biệt là trong môi trường học tập và làm việc. Hy vọng rằng thông qua bài viết này, bạn đã có cái nhìn tổng quan và sâu sắc hơn về tỷ lệ 2 phần 3 trong nhiều lĩnh vực khác nhau.