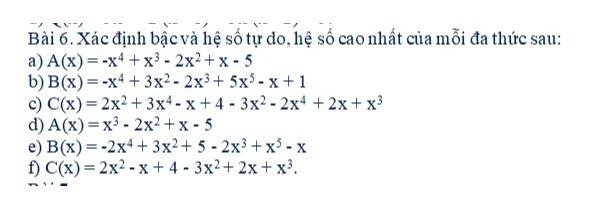Giới thiệu về khái niệm hệ số không chứa biến
Trong toán học, đặc biệt trong lĩnh vực đại số, có một khái niệm quan trọng mà học sinh thường gặp phải khi nghiên cứu về đa thức. Khái niệm này chủ yếu đề cập đến giá trị cố định của một hàm số mà không bị ảnh hưởng bởi các biến trong hàm số đó. Việc hiểu rõ về khái niệm này không chỉ giúp học sinh nắm vững lý thuyết mà còn áp dụng để giải quyết các bài toán liên quan một cách hiệu quả. Chúng ta sẽ cùng khám phá khái niệm này thông qua các ví dụ cụ thể, định nghĩa, và ứng dụng của nó.
Khái niệm cơ bản
Hệ số không chứa biến thực chất là một thành phần trong một đa thức mà không có bất kỳ biến nào đi kèm. Để dễ hình dung, hãy xem xét một đa thức tổng quát có dạng:
\[ f(x) = a_nx^n + a_{n-1}x^{n-1} + \ldots + a_1x + a_0 \]
Trong đó, \( a_n, a_{n-1}, \ldots, a_1, a_0 \) là các hệ số của đa thức, và \( a_0 \) chính là giá trị mà chúng ta gọi là hệ số không chứa biến. Điều này có nghĩa là khi giá trị của biến \( x \) bằng 0, giá trị của hàm số \( f(x) \) sẽ trở thành \( a_0 \). Chính vì lý do này, giá trị của hệ số không chứa biến trong một đa thức rất quan trọng và thường được các nhà toán học sử dụng để phân tích tính chất của hàm số.
Đặc điểm của hệ số không chứa biến
Hệ số không chứa biến và độ bậc của đa thức
Để hiểu rõ hơn về hệ số không chứa biến, chúng ta cần nắm rõ mối quan hệ giữa hệ số này và độ bậc của đa thức. Độ bậc của một đa thức được xác định bởi bậc cao nhất của biến trong đa thức đó. Ví dụ, trong đa thức:
\[ f(x) = 3x^4 + 5x^2 - 7x + 8 \]
Bậc cao nhất là 4, hệ số không chứa biến là 8. Hệ số không chứa biến thường có thể cho chúng ta thông tin về giá trị của hàm số khi biến bằng 0. Điều này có ý nghĩa quan trọng trong các ứng dụng thực tiễn như trong việc tính toán và dự đoán.
Hệ số không chứa biến trong các bài toán
Một trong những ứng dụng rõ ràng nhất của hệ số không chứa biến là trong việc giải quyết các bài toán liên quan đến đa thức. Ví dụ, khi một bài toán yêu cầu xác định giá trị của một đa thức tại một điểm nhất định, việc xác định hệ số không chứa biến sẽ giúp đơn giản hóa bài toán.
Giả sử chúng ta có một đa thức:
\[ g(x) = 2x^3 - 4x^2 + 3x + 10 \]
Khi \( x = 0 \), ta sẽ có \( g(0) = 10 \). Ở đây, 10 chính là giá trị của hệ số không chứa biến trong đa thức này.
Phân loại và ứng dụng của hệ số không chứa biến
Phân loại các hệ số trong đa thức
Trong một đa thức, không chỉ có một hệ số không chứa biến mà còn có nhiều loại hệ số khác như hệ số cao nhất, hệ số bậc thấp, và hệ số bậc 1. Mỗi loại hệ số này đều có vai trò và ý nghĩa riêng trong việc phân tích và giải quyết các bài toán.
- Hệ số cao nhất: Là hệ số của hạng tử có bậc cao nhất trong đa thức. Ví dụ, trong đa thức \( h(x) = 7x^5 - 3x^4 + 2 \), hệ số cao nhất là 7.
- Hệ số bậc thấp: Là hệ số của các hạng tử có bậc thấp hơn. Hệ số này có thể cung cấp thông tin về hình dạng của đồ thị hàm số.
- Hệ số không chứa biến: Như đã nói ở trên, giá trị không phụ thuộc vào biến và thường được dùng để tính giá trị của đa thức tại \( x = 0 \).
Ứng dụng trong thống kê và khoa học
Ngoài việc sử dụng trong toán học cơ bản, khái niệm hệ số không chứa biến còn được áp dụng trong các lĩnh vực như thống kê, khoa học máy tính và kinh tế học. Chẳng hạn, trong thống kê, hệ số không chứa biến được sử dụng để tính toán các chỉ số thống kê như trung bình, phương sai.
Tính toán trong các bài toán thực tế
Hệ số không chứa biến cũng có thể được ứng dụng trong các bài toán tối ưu hóa trong kinh tế. Một mô hình kinh tế có thể được biểu diễn dưới dạng đa thức, trong đó hệ số không chứa biến cho biết giá trị cơ bản của tham số khi các yếu tố khác không tác động.
Kết luận
Như vậy, khái niệm hệ số không chứa biến là một phần không thể thiếu trong việc nghiên cứu và phân tích đa thức. Qua các nội dung đã đề cập, chúng ta đã hiểu rõ hơn về định nghĩa, đặc điểm, phân loại và ứng dụng của hệ số này trong toán học cũng như các lĩnh vực khác. Việc nắm vững khái niệm này không chỉ giúp học sinh nâng cao khả năng tư duy logic mà còn là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai.
Hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin bổ ích và cần thiết để bạn có thể áp dụng vào việc học tập và nghiên cứu của mình. Hãy tiếp tục khám phá thế giới của toán học và các khái niệm thú vị khác mà nó mang lại!