Tính diện tích tam giác vuông và các công thức liên quan
Tam giác là một trong những hình học cơ bản mà chúng ta thường gặp không chỉ trong toán học mà còn trong đời sống hàng ngày. Đặc biệt, tam giác vuông là một trong những loại tam giác được học nhiều nhất do những ứng dụng rộng rãi của nó trong nhiều lĩnh vực. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về cách tính diện tích tam giác vuông và những khái niệm liên quan.
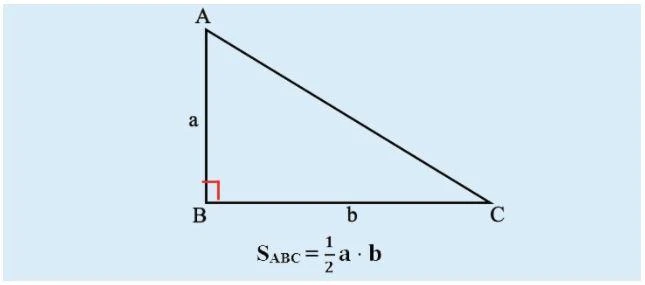
Tam giác vuông là gì?
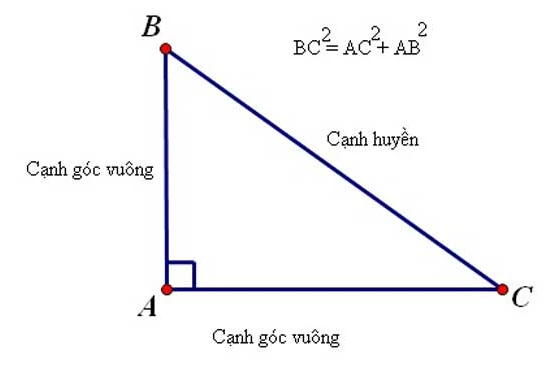
Tam giác vuông là hình tam giác có một góc vuông (góc 90 độ). Đặc điểm đặc biệt của tam giác vuông là cạnh đối diện với góc vuông gọi là cạnh huyền (cạnh dài nhất), trong khi hai cạnh còn lại được gọi là cạnh góc vuông. Tổng của hai góc còn lại trong tam giác vuông sẽ luôn bằng 90 độ.
- Công thức Pythagore: Một trong những tính chất quan trọng của tam giác vuông là định lý Pythagore. Định lý này nói rằng bình phương độ dài của cạnh huyền bằng tổng bình phương độ dài của hai cạnh góc vuông. Cụ thể:
\[
c^2 = a^2 + b^2
\]
Trong đó:
- \( c \) là chiều dài cạnh huyền.
- \( a \) và \( b \) là chiều dài của hai cạnh góc vuông.
Cách tính diện tích tam giác vuông
Diện tích của tam giác vuông được tính theo công thức đơn giản:
\[
S = \frac{1}{2} \times a \times b
\]
Trong đó:
- \( S \) là diện tích.
- \( a \) và \( b \) là độ dài của hai cạnh góc vuông.
Ví dụ minh hoạ
- Ví dụ 1: Nếu một tam giác vuông có cạnh góc vuông \( a = 3 \) cm và \( b = 4 \) cm. Tính diện tích tam giác này.
Công thức:
\[
S = \frac{1}{2} \times 3 \times 4 = 6 \text{ cm}^2
\]
- Ví dụ 2: Tam giác vuông có hai cạnh góc vuông lần lượt là 5 m và 12 m.
Công thức:
\[
S = \frac{1}{2} \times 5 \times 12 = 30 \text{ m}^2
\]
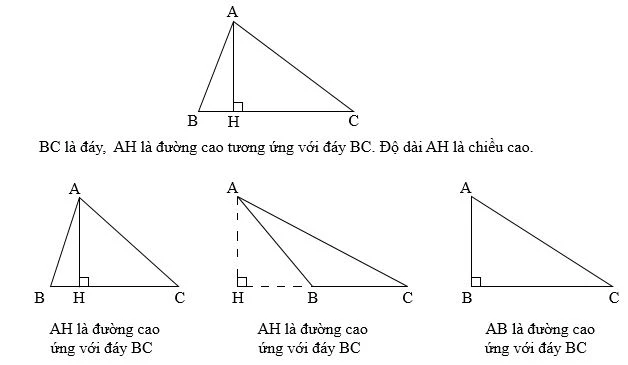
Cách khác tính diện tích tam giác vuông
Ngoài việc sử dụng công thức tính diện tích trên, có thể tính diện tích tam giác vuông thông qua cạnh huyền và chiều cao. Nếu bạn biết chiều dài của cạnh huyền và chiều cao tương ứng, bạn có thể áp dụng công thức sau:
\[
S = \frac{1}{2} \times c \times h
\]
Trong đó:
- \( c \) là chiều dài cạnh huyền.
- \( h \) là chiều cao kẻ từ đỉnh góc vuông xuống cạnh huyền.
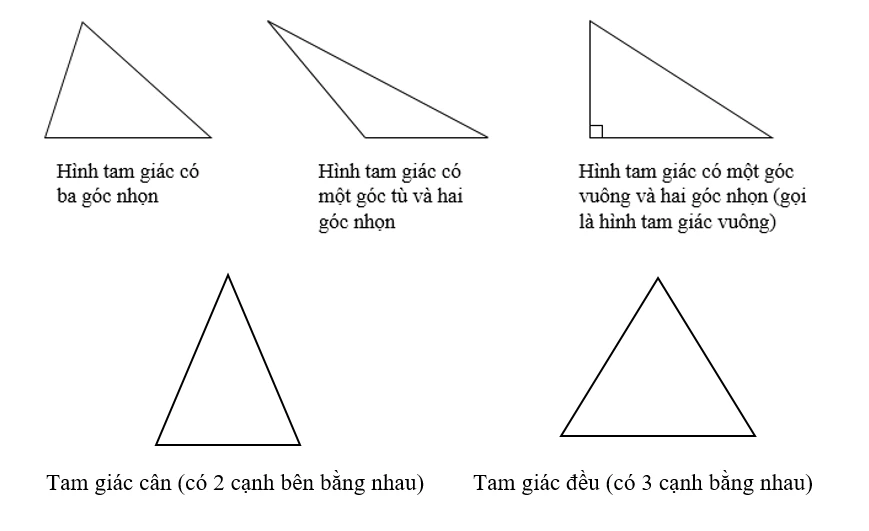
Các loại tam giác khác và công thức tính diện tích
Ngoài tam giác vuông, còn rất nhiều loại tam giác khác mà bạn cũng cần nắm rõ cách tính diện tích của chúng.
1. Tam giác đều
Tam giác đều là loại tam giác có cả 3 cạnh đều nhau. Công thức tính diện tích cho tam giác đều là:
\[
S = \frac{\sqrt{3}}{4} \times a^2
\]
Trong đó \( a \) là độ dài cạnh của tam giác.
2. Tam giác cân
Tam giác cân là hình tam giác có hai cạnh bằng nhau. Công thức tính diện tích cho tam giác cân là:
\[
S = \frac{1}{2} \times a \times h
\]
Trong đó:
- \( a \) là độ dài cạnh đáy.
- \( h \) là chiều cao.
3. Tam giác thường
Tam giác có các cạnh và góc không đều được gọi là tam giác thường. Công thức tính diện tích cho tam giác thường là:
\[
S = \frac{1}{2} \times a \times h
\]
Một số dạng bài tập tính diện tích tam giác
Dạng 1: Tính diện tích tam giác với chiều cao và cạnh đáy
- Bài tập 1: Tính diện tích tam giác có chiều cao 10 cm và cạnh đáy 15 cm.
Giải:
\[
S = \frac{1}{2} \times 10 \times 15 = 75 \text{ cm}^2
\]
Dạng 2: Tính chiều cao khi biết diện tích và chiều dài cạnh đáy
- Bài tập 2: Tính chiều cao của tam giác có diện tích 80 cm² và chiều dài cạnh đáy 16 cm.
Giải:
\[
h = \frac{S \times 2}{a} = \frac{80 \times 2}{16} = 10 \text{ cm}
\]
Lời kết
Việc hiểu biết về tính diện tích tam giác, đặc biệt là tam giác vuông, không chỉ mang lại kiến thức toán học cơ bản mà còn ứng dụng trong nhiều lĩnh vực khác nhau như kỹ thuật, xây dựng và kiến trúc. Hy vọng rằng bài viết này cung cấp cho bạn một cái nhìn toàn diện về các loại tam giác và công thức tính diện tích liên quan. Hãy thực hành nhiều bài tập để nâng cao kỹ năng toán học của bạn!

















