Với chương trình học Toán lớp 9, cách chứng minh vuông góc trong đường tròn là một trong những phần quan trọng không thể bỏ qua. Trong bài viết này, chúng ta sẽ cùng khám phá các khái niệm cơ bản, tính chất cần nhớ cũng như các bước chi tiết để chứng minh vuông góc trong các bài toán hình học liên quan đến đường tròn.
Hãy cùng nhau bắt đầu nhé!
1. Khái Niệm Cơ Bản Về Đường Tròn và Vuông Góc
1.1 Đường Tròn
Đường tròn là một hình phẳng được tạo thành bởi tất cả các điểm có khoảng cách bằng nhau đến một điểm đã chọn gọi là
tâm(O). Khoảng cách này gọi là
bán kính (r).
1.2 Vuông Góc
Vuông góc là một khái niệm rất quen thuộc. Hai đường thẳng được coi là vuông góc với nhau khi chúng tạo thành một góc 90 độ hay một thiết lập mà tại đó các đường thẳng này cắt nhau tại một điểm duy nhất và góc tạo thành là góc vuông.
2. Các Tính Chất Cần Nhớ Khi Chứng Minh Vuông Góc Trong Đường Tròn
2.1 Tính Chất Vuông Góc Của Tiếp Tuyến
- Tiếp tuyến tại một điểm của đường tròn luôn vuông góc với dây kính vẽ từ tâm đến điểm tiếp xúc.
2.2 Tính Chất Đường Kính và Dây Cung
- Đường kính của đường tròn sẽ vuông góc với dây cung nếu nó đi qua trung điểm của dây cung đó.
2.3 Góc Nội Tiếp và Góc Ở Tâm
- Góc nội tiếp chắn cung bằng một nửa góc ở tâm chắn cung đó. Điều này giúp ích rất nhiều trong việc chứng minh các mối quan hệ vuông góc.
3. Các Bước Chứng Minh Vuông Góc Trong Đường Tròn Lớp 9
3.1 Chứng Minh Tiếp Tuyến Vuông Góc Với Bán Kính
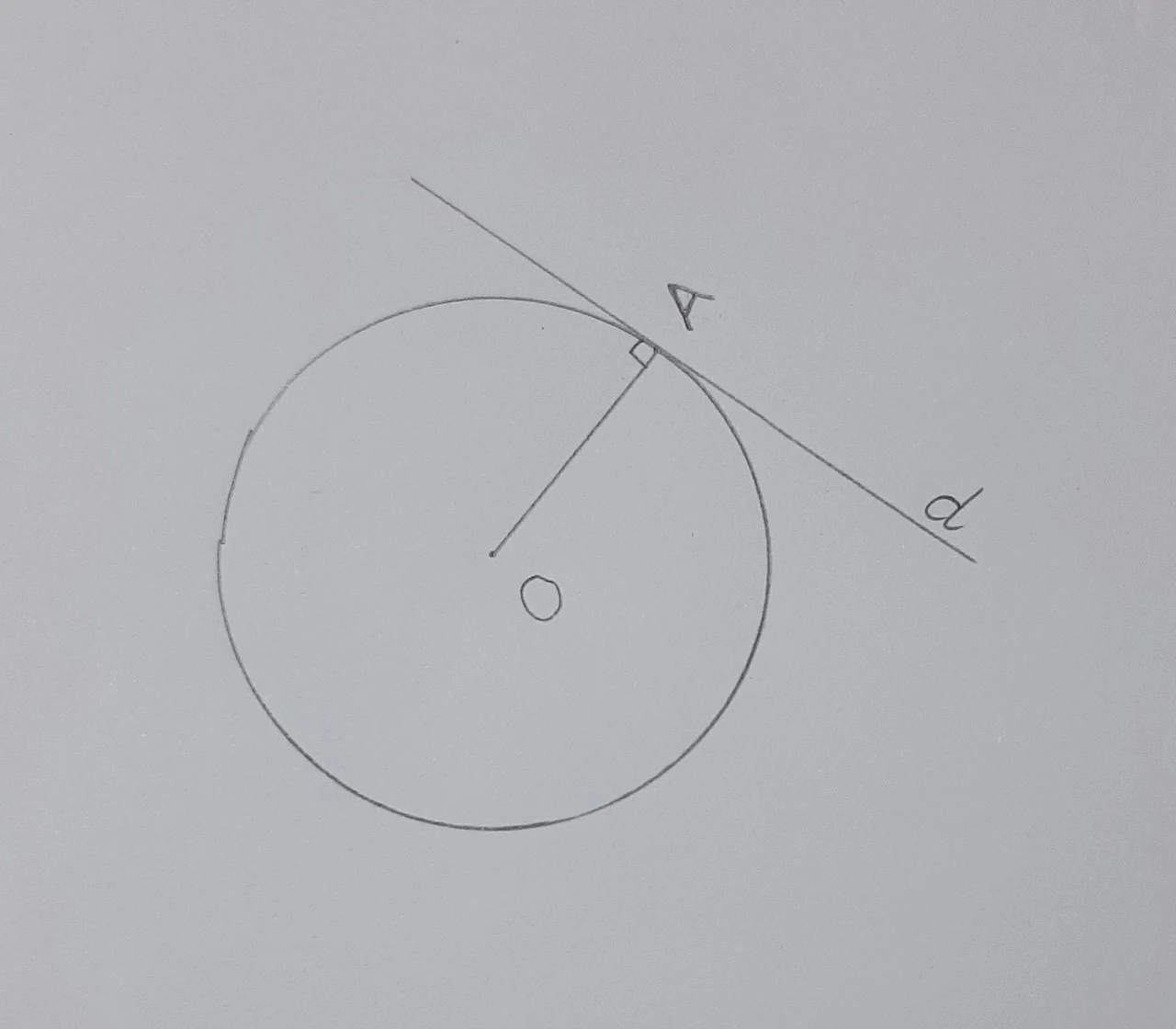
Đề bài: Cho đường tròn (O) và điểm A nằm trên đường tròn. Gọi tiếp tuyến tại A là d. Chứng minh d vuông góc với OA.
Giải:
- Vẽ đường tròn (O) với bán kính OA.
- Vẽ tiếp tuyến d tại điểm A.
- Xét tam giác vuông OAD với điểm D nằm trên tiếp tuyến d sao cho OD vuông góc với d tại A.
- Theo định lý hình học, tiếp tuyến d vuông góc với bán kính OA tại điểm A.
3.2 Chứng Minh Đường Kính Vuông Góc Với Dây Cung
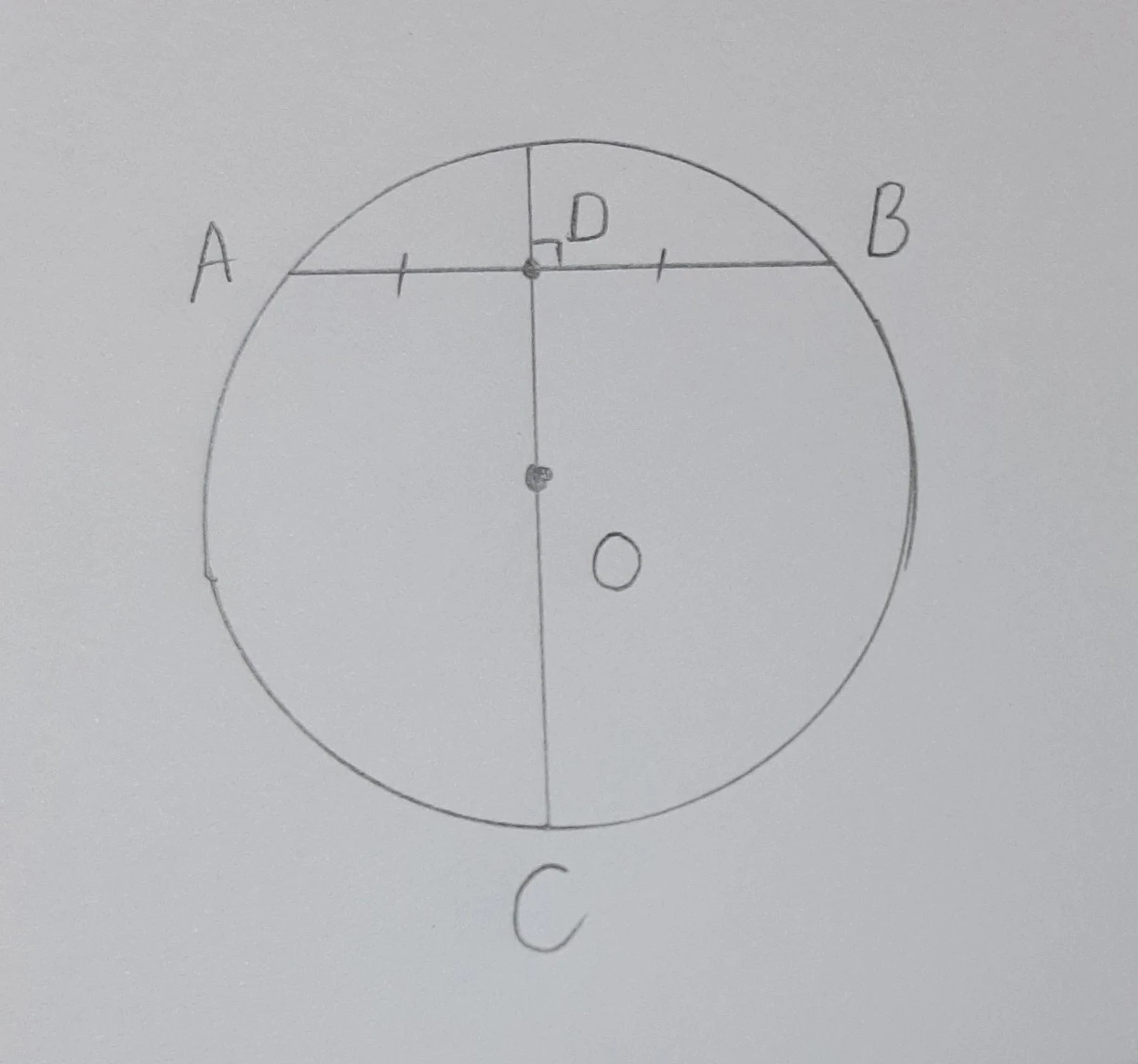
Đề bài: Cho đường tròn (O) và dây cung AB. Gọi D là trung điểm của AB và vẽ đường kính CD. Chứng minh CD vuông góc với AB.
Giải:
- Vẽ đường tròn (O) với dây cung AB và đánh dấu D là trung điểm của AB.
- Vẽ đường kính CD.
- Nhận thấy rằng OD là trung trực của đoạn AB.
- Theo tính chất của đường kính, CD sẽ vuông góc với AB tại điểm D.
3.3 Chứng Minh Vuông Góc Từ Góc Nội Tiếp và Góc Ở Tâm
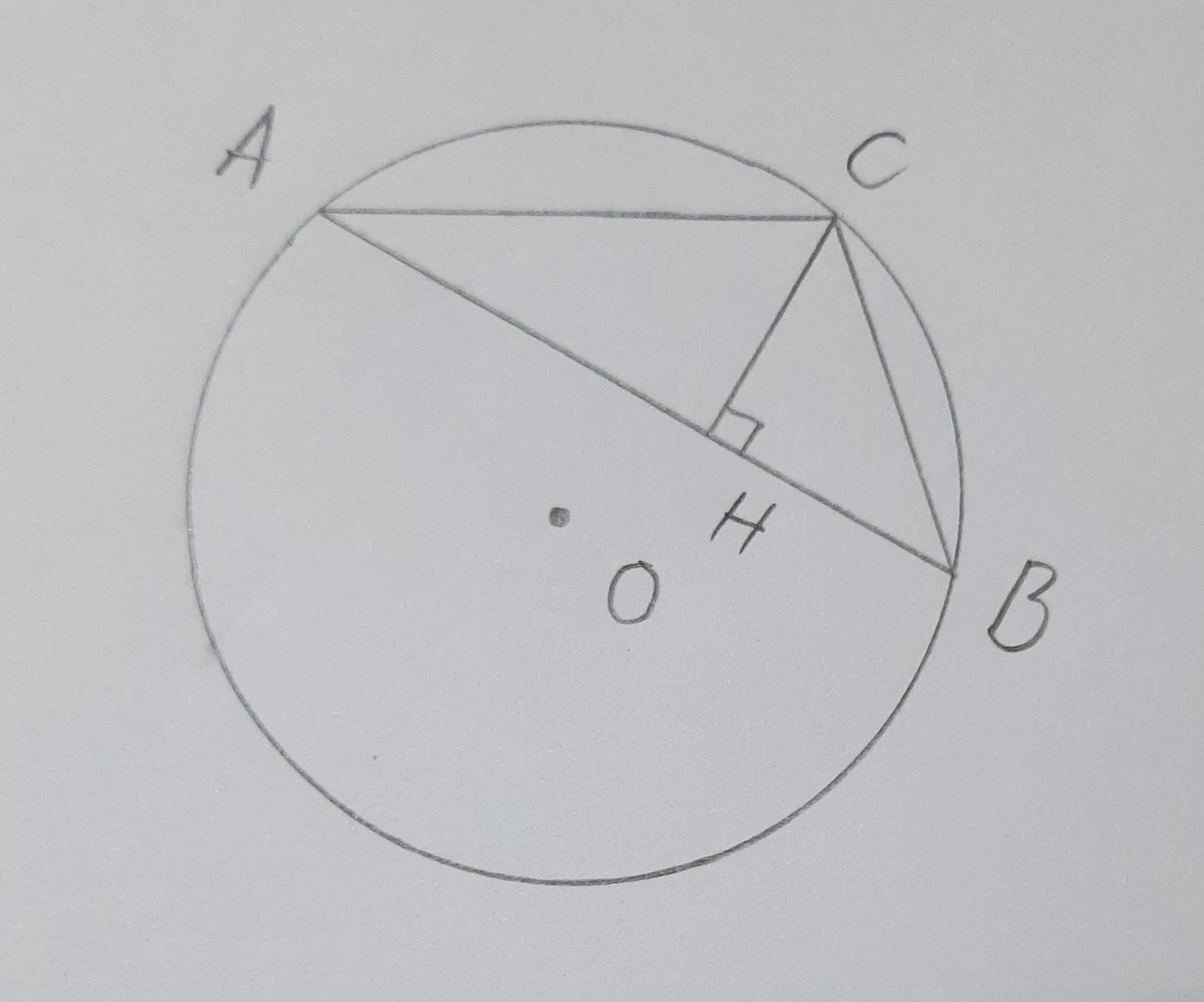
Đề bài: Cho đường tròn (O) với dây cung AB và góc nội tiếp ∠ACB chắn cung AB. Gọi H là hình chiếu vuông góc của C lên AB. Chứng minh CH vuông góc với AB.
Giải:
- Vẽ đường tròn (O), dây cung AB và điểm C sao cho ∠ACB chắn cung AB.
- Vẽ hình chiếu vuông góc của C lên AB, gọi điểm hình chiếu là H.
- Dựa vào định lý góc nội tiếp: ∠ACB = 1/2 ∠AOB, từ đó suy ra góc ∠AOB ở tâm bộ đường tròn.
- Xét triangle CHB vuông tại H, do CH là đường vuông góc từ C tới AB.
4. Một Số Lưu Ý Khi Thực Hành Chứng Minh Vuông Góc
Để việc chứng minh trở nên dễ dàng hơn, các em cần chú ý những điểm sau:
- Nắm vững kiến thức cơ bản: Các tính chất và định lý về đường tròn rất cần thiết.
- Thực hành nhiều bài tập: Giải quyết các bài tập liên quan sẽ giúp các em ghi nhớ hơn.
- Khéo léo trong việc vẽ hình: Một hình vẽ chính xác sẽ hỗ trợ rất lớn trong việc chứng minh và hiểu các mối quan hệ.
5. Kết Luận
Trong bài viết hôm nay, chúng ta đã điểm qua các khái niệm cơ bản về đường tròn và cách chứng minh vuông góc liên quan đến sự cấu trúc của nó. Bằng cách hiểu rõ các tính chất và áp dụng chúng vào trong các bài toán, chắc chắn rằng các em sẽ có thể giải quyết được các vấn đề hình học một cách dễ dàng và nhanh chóng.
Hy vọng rằng bài viết này sẽ là tài liệu hữu ích giúp các em học sinh lớp 9 học tập hiệu quả hơn. Nếu còn thắc mắc hoặc cần thêm thông tin, hãy để lại câu hỏi dưới bài viết để được giải đáp nhé!
Ngoài ra, đừng quên tham khảo các tài liệu học tập khác của
TKbooks.vn để tự tin hơn trong kỳ thi sắp tới!















