Cái Nhìn Tổng Quát Về Trực Tâm Tam Giác
Tam giác là một trong những hình học cơ bản nhất trong toán học, và trực tâm là một trong những điểm đặc biệt của tam giác. Được định nghĩa là giao điểm của ba đường cao, trực tâm không chỉ có ý nghĩa lý thuyết mà còn đóng vai trò quan trọng trong các bài toán hình học thực tế.
Trực Tâm Là Gì?
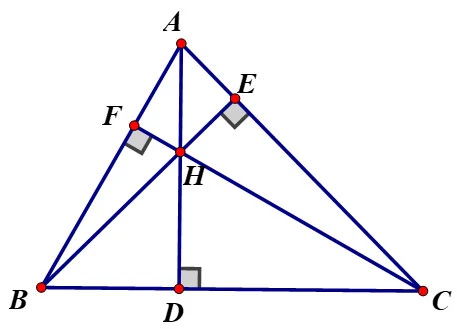
- Định Nghĩa: Trực tâm của một tam giác là giao điểm của ba đường cao của tam giác đó. Đường cao được xác định là đoạn thẳng từ mỗi đỉnh của tam giác vuông góc với cạnh đối diện.
- Hình Ảnh Minh Họa: (Chèn hình ảnh minh họa về một tam giác và các đường cao của nó).
Phân Loại Trực Tâm Theo Loại Tam Giác
- Tam Giác Nhọn: Nếu tam giác là tam giác nhọn, trực tâm sẽ nằm bên trong tam giác.
- Tam Giác Vuông: Nếu tam giác vuông tại một đỉnh, trực tâm trùng với đỉnh vuông đó.
- Tam Giác Tù: Nếu tam giác là tam giác tù, trực tâm sẽ nằm bên ngoài tam giác.
Cách Xác Định Trực Tâm Của Tam Giác
Các Bước Để Chứng Minh Trực Tâm
Bước 1: Xác định Đường Cao
- Với tam giác có đỉnh A, B, C, hãy vẽ các đường vuông góc từ A, B, C đến các cạnh BC, AC, AB.
- Gọi các điểm vuông góc là D, E, F. Như vậy, AD sẽ là đường cao từ A đến BC, BE từ B đến AC, và CF từ C đến AB.
Bước 2: Tìm Giao Điểm
- Ta cần tìm giao điểm của ba đường cao AD, BE và CF. Điểm giao nhau này chính là trực tâm H của tam giác ABC.
Hình Vẽ Minh Họa
- (Chèn hình ảnh minh họa về các đường cao và điểm trực tâm của tam giác ABC).
Một Số Tính Chất Của Trực Tâm
- Tính Chất Đối Xứng: Trong tam giác đều, trực tâm trùng với trọng tâm và trung điểm của các cạnh.
- Tính Chất Về Độ Dài: Độ dài của đường cao có thể được tính bằng công thức, tùy thuộc vào loại tam giác (vuông, nhọn, tù).
- Tính Chất Về Góc: Trực tâm có một số liên hệ đặc biệt với các góc của tam giác.
Một Vài Bài Tập Chứng Minh Trực Tâm
Bài Tập Lớp 8
Ví dụ 1: Cho tam giác ABC không vuông. Hãy chỉ ra các đường cao và trực tâm của tam giác.
Hướng Dẫn Giải:
- Xác định các đường cao từ A, B, C đến các cạnh đối diện.
- Tìm giao điểm của chúng để xác định trực tâm H.
Bài Tập Lớp 9
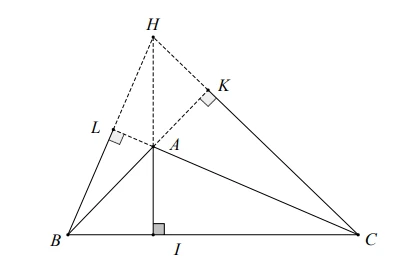
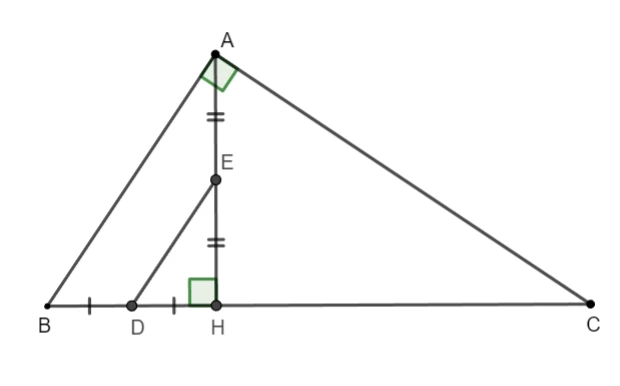
Ví dụ 2: Cho tam giác ABC vuông tại A, đường cao AH. Hãy xác định trực tâm tam giác ADE khi D là trung điểm của BH.
Hướng Dẫn Giải:
- Tính toán các đoạn thẳng và góc tại các điểm liên quan.
- Chứng minh rằng góc CK là một góc vuông, từ đó chỉ ra vị trí của trực tâm.
Các Bài Tập Nâng Cao
Ví dụ Chứng Minh 1
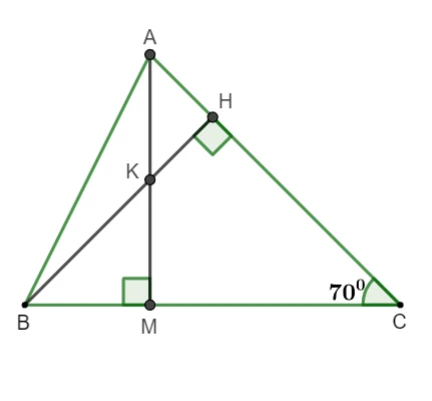
Đề bài: Cho tam giác ABC cân tại A có góc C = 70°. Hãy chứng minh CK ⊥ AB và tìm góc HKM.
Hướng Dẫn:
- Xác minh rằng AM là đường cao.
- Sử dụng các tính chất của tam giác để tính góc HKM.
Ví dụ Chứng Minh 2
Đề bài: Cho tam giác ABC có đường cao BH, tìm hiểu mối liên hệ giữa điểm K và trực tâm của tam giác dấu hiệu đặc biệt.
Hướng Dẫn:
- Phân tích mối quan hệ giữa các cạnh và góc trong tam giác.
- Sử dụng các định lý hình học để chứng minh mối liên hệ và tìm trực tâm.
Kết Luận
Chứng minh trực tâm trong tam giác không chỉ giúp chúng ta hiểu rõ hơn về hình học mà còn rèn luyện tư duy logic và khả năng giải quyết vấn đề. Để thành thạo kỹ năng này, người học cần thực hành qua nhiều bài tập khác nhau và nắm vững các định lý căn bản trong hình học. Hãy không ngừng luyện tập và khám phá những điều thú vị từ hình học, nơi những con số và hình dạng gặp nhau để mở ra những ý tưởng mới.
Việc nắm vững các cách chứng minh và áp dụng linh hoạt sẽ không chỉ củng cố nền tảng kiến thức mà còn mở ra nhiều cơ hội khám phá trong toán học và các lĩnh vực liên quan.

















