Hình thang, mặc dù là một trong những hình học cơ bản, thực sự bao gồm nhiều tính chất và định lý quan trọng mà mọi học sinh cần nắm vững. Trong bài viết này, chúng tôi sẽ giúp bạn tìm hiểu về hình thang, các tính chất cũng như cách chứng minh hình thang một cách chi tiết và dễ hiểu. Hãy cùng khám phá!
I. Khái Niệm và Tính Chất Của Hình Thang
1. Hình Thang Là Gì?
Hình thang là một tứ giác có hai cạnh đối song song. Cụ thể hơn, nếu gọi hình thang là ABCD, thì điều kiện để ABCD là hình thang là AB // CD.
2. Tính Chất Của Hình Thang
Một hình thang có một số tính chất quan trọng mà chúng ta cần ghi nhớ:
- Tính chất 1: Hai góc kề ở một cạnh bên của hình thang có tổng bằng 180 độ.
- Ví dụ: Trong hình thang ABCD, nếu AB // CD thì ta có:
- Góc A + Góc D = 180°
- Góc B + Góc C = 180°
- Tính chất 2: Hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên sẽ song song và bằng nhau.
- Nếu AB = CD thì AD = BC và AD // BC.
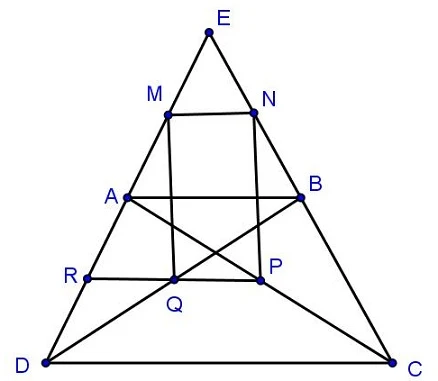
- Tính chất 3: Đường trung bình của hình thang là đường thẳng nối hai trung điểm của hai cạnh bên. Đường trung bình sẽ song song với hai cạnh đáy và có độ dài bằng 1/2 tổng độ dài của hai cạnh đáy.
3. Cách Chứng Minh Hình Thang
Chúng ta có thể chứng minh hình thang bằng một số cách khác nhau:
Cách 1: Chứng Minh Có Một Cặp Cạnh Đối Song Song
Để chứng minh tứ giác là hình thang, ta cần chỉ ra rằng có một cặp cạnh đối song song.
Cách 2: Chứng Minh Tổng Hai Góc Kề Một Cạnh Bên Bằng 180 Độ
Cách này dựa vào việc sử dụng các tính chất của góc trong hình học.
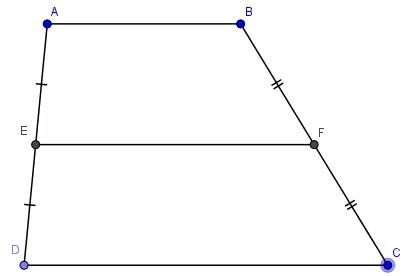
Ví Dụ Minh Họa
Hãy xem xét một ví dụ cụ thể để hiểu rõ hơn về cách chứng minh hình thang. Giả sử chúng ta có tứ giác ABCD và biết rằng AB // CD.
- Xét góc A và góc D: Nếu tổng của hai góc này bằng 180 độ, tức là Góc A + Góc D = 180°, ta có thể kết luận rằng ABCD là hình thang.
II. Hình Thang Cân
1. Định Nghĩa Hình Thang Cân
Hình thang cân là hình thang có hai góc kề một cạnh đáy bằng nhau. Đây được coi là một trường hợp đặc biệt của hình thang.
2. Tính Chất Của Hình Thang Cân
- Tính chất 1: Trong một hình thang cân, hai cạnh bên là bằng nhau.
- Tính chất 2: Hai đường chéo của hình thang cân cũng bằng nhau.
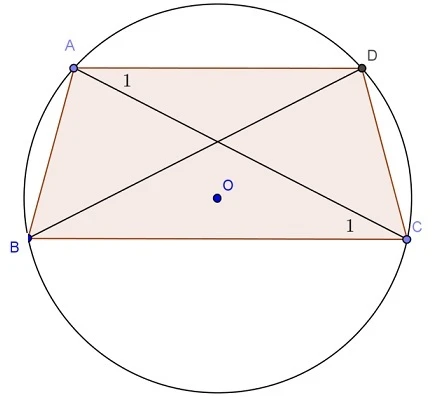
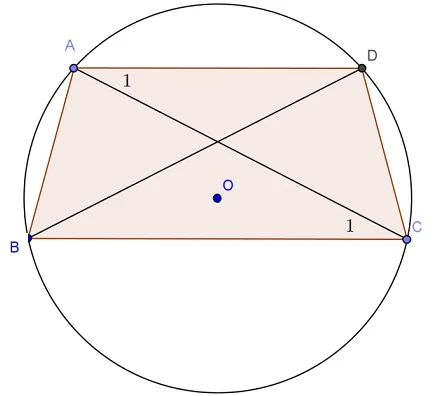
- Tính chất 3: Hình thang cân có khả năng nội tiếp trong một đường tròn.
3. Cách Chứng Minh Hình Thang Cân
Cách 1: Chứng Minh Hai Góc Kề Một Cạnh Đáy Bằng Nhau
Nếu một tứ giác có hai góc kề một cạnh đáy bằng nhau, thì tứ giác đó là hình thang cân.
Cách 2: Chứng Minh Hai Cạnh Bên Bằng Nhau
Nếu hai cạnh bên của một hình thang bằng nhau, thì đó là hình thang cân.
Cách 3: Chứng Minh Hai Đường Chéo Bằng Nhau
Nếu hai đường chéo của tứ giác là bằng nhau, thì tứ giác đó là hình thang cân.
Ví Dụ Minh Họa
Một ví dụ để minh họa cách chứng minh hình thang cân là tứ giác ABCD với AB // CD và các góc C = D. Ta cần chứng minh rằng ABCD là hình thang cân.
- Ta biết rằng nếu góc C = góc D, theo định nghĩa của hình thang cân, ta khẳng định rằng ABCD là hình thang cân.
- Điều này có thể được chứng minh bằng cách sử dụng định lý về các góc đối diện.
Kết Luận
Trong bài viết này, chúng tôi đã tổng hợp những kiến thức cơ bản và cần thiết liên quan đến hình thang và hình thang cân, bao gồm cả cách chứng minh. Những thông tin này không chỉ giúp bạn hiểu rõ hơn về hình thang mà còn giúp bạn làm bài tập và thi cử dễ dàng hơn.
Nếu bạn có bất kỳ câu hỏi nào hoặc cần thêm thông tin, hãy tham khảo Gia Sư Việt để được hỗ trợ tốt nhất. Chúng tôi luôn sẵn sàng giúp bạn nâng cao trình độ học tập. Đừng quên theo dõi chúng tôi để cập nhật thêm nhiều kiến thức hữu ích khác nhé!

















